ヒューリスティックコンテスト、楽しんでますか？私は楽しんでいます。最近企業AHCなんかも続々と出てきて、これからどんどん盛り上がってくれるんじゃないかと期待しています。

とはいえ、ヒューリスティックコンテスト特有の取っつきづらさがあるのも確かです。「どこから手を付けていいか分からない……」「AHC後のTLに焼きなましとか2-optとか流れてきたけど何が何だか……」と思われた方も多くいらっしゃるのではないでしょうか？

AHC006は巡回セールスマン問題を発展させた問題なので、確かに2-optを使った焼きなましができると有利ではあります。しかし、専門知識がないと戦えないかというと全くそんなことはありません。

この記事では、AtCoder Heuristic Contest 006 (AHC006)を題材として、

焼きなまし → 使いません
ビームサーチ → 使いません
2-opt → もちろん使いません

という縛りの中、全ての基本である直感に頼った貪欲だけで順位表の2ページ目を目指します。

伝えたいことを3行で
対象読者
問題概要
テンプレコード
貪欲その1
貪欲その2
- 別の貪欲を試してみる
- アルゴの知識で高速化する
おわりに

伝えたいことを3行で

貪欲だけでもいい順位まで行けるよ！
ビジュアライザは改善点の宝庫だよ！
意外とABCで学んだアルゴリズムの使いどころがあるよ！

対象読者

ヒューリスティックコンテスト未経験～レーティング（β）2000くらい？を対象にしています。それより強い人はどんどんこの記事にツッコんでください。

また、アルゴリズム（ABCとか）のレートが緑くらいあるとスムーズに読めるかなと思います。茶色でもある程度は大丈夫かなとは思いますが、灰色だとちょっと難しいかもしれません。ご了承ください。

サンプルコードはPythonで書かれています。他言語メインの人は頑張って読んでください。私も慣れない中頑張って書いたので……。

問題概要

1000個ある注文の中から50個を選んで、できるだけ早く料理の配達を終わらせてね！

atcoder.jp

全探索できれば厳密解が求められますが、配達ルートの候補数が $O\left(\frac{_N C_m (2m)!}{2^m}\right)$ 通りくらい？あってまあ無理そうです。というわけで、厳密解が出ないという前提でできるだけ良い解を求めていきます。

テンプレコード

こんな感じのテンプレを作ってみました。

ORDER_COUNT = 1000  # 注文の数
PICKUP_COUNT = 50  # 選択する必要のある注文の数
CENTER = 400  # AtCoderオフィスのx,y座標


def read_input():
    """
    各点の座標を読み込む。
    """
    rest_x = []  # レストランのx座標
    rest_y = []  # レストランのy座標
    dest_x = []  # 配達先のx座標
    dest_y = []  # 配達先のy座標

    for _ in range(ORDER_COUNT):
        x0, y0, x1, y1 = map(int, input().split())
        rest_x.append(x0)
        rest_y.append(y0)
        dest_x.append(x1)
        dest_y.append(y1)

    return rest_x, rest_y, dest_x, dest_y


def solve(rest_x, rest_y, dest_x, dest_y):
    """
    0, 1, 2, ..., 49番目のレストラン → 0, 1, 2, ..., 49番目の配達先を順に回る
    """
    orders = list(range(PICKUP_COUNT))
    result_x = [CENTER]
    result_y = [CENTER]
    result_x.extend(rest_x[:PICKUP_COUNT])
    result_x.extend(dest_x[:PICKUP_COUNT])
    result_y.extend(rest_y[:PICKUP_COUNT])
    result_y.extend(dest_y[:PICKUP_COUNT])
    result_x.append(CENTER)
    result_y.append(CENTER)
    return orders, result_x, result_y


def output(orders, x, y):
    """
    解を出力する。
    """
    orders = [str(i + 1) for i in orders]
    coordinates = [f"{x} {y}" for x, y in zip(x, y)]
    print(f"{len(orders)} {' '.join(orders)}")
    print(f"{len(coordinates)} {' '.join(coordinates)}")


def dist(x0, y0, x1, y1):
    """
    (x0, y0)と(x1, y1)のマンハッタン距離を求める
    """
    return abs(x0 - x1) + abs(y0 - y1)


rest_x, rest_y, dest_x, dest_y = read_input()
orders, x, y = solve(rest_x, rest_y, dest_x, dest_y)
output(orders, x, y)

solve()関数はレストランの座標のリスト（rest_x, rest_y）と配達先の座標のリスト（dest_x, dest_y）を受け取り、選択した注文番号（orders）と配達ルート（result_x, result_y）を返す関数です。この関数を今後作り込んでいきます。これ以外の関数は最後まで書き換えません。

ちなみにテンプレコードは番号1～50の注文を順に回るアルゴリズムになっていて、これを提出すると183,038点になります。参加者549人中511位相当です。

atcoder.jp

ビジュアライザはこんな感じ。赤がレストラン、緑が配達先です。*1

f:id:terry_u16:20211124234512p:plain — ビジュアライザ (seed=0)

貪欲その1

とりあえず貪欲をする

全ての基本、貪欲をしましょう。

ビジュアライザを見てみてもまあなんだかよく分からないんですが、とりあえずあっちこっち行っていて効率が悪そうに見えます。配達中の高橋君の気持ちになってみると、はるか遠くにあるレストランよりも今近くに見えているレストランに行きたくなります（私はなりました）。レストランの後に配達先を……と考えていくと大変なので、とりあえずレストランを近い順に50軒回ってから配達先を近い順に50軒回っていくことにしましょう。*2

整理すると、以下のようなアルゴリズムになります。

高橋君は最初オフィスにいます。
訪問したレストランが50軒に達するまで、今いる場所から一番近いレストランに移動することを繰り返します。
受けた注文を捌ききるまで、今いる場所から一番近い配達先に移動することを繰り返します。
オフィスに帰ります。

コードは以下の通りです。solve()関数の中身だけ表示しています。

def solve(rest_x, rest_y, dest_x, dest_y):
    """
    今いる場所に最も近いレストランを50個貪欲に回り、
    その後最も近い配達先を貪欲に回る
    """
    orders = []
    result_x = [CENTER]
    result_y = [CENTER]

    # 採用する注文の候補（1～1000番の全てを候補とする）
    candidates = list(range(ORDER_COUNT))

    # 現在位置をオフィスにセット
    current_x = CENTER
    current_y = CENTER

    # 今いる場所に最も近いレストランを50個貪欲に回る
    for _ in range(PICKUP_COUNT):
        # 候補の中から、一番近いレストランを探す
        min_dist = 1000000007
        min_index = 998244353

        for i, v in enumerate(candidates):
            d = dist(current_x, current_y, rest_x[v], rest_y[v])
            if d < min_dist:
                min_dist = d
                min_index = i

        # レストランの注文番号
        v = candidates[min_index]

        # 解を更新
        orders.append(v)
        result_x.append(rest_x[v])
        result_y.append(rest_y[v])

        # 現在位置を更新
        current_x = rest_x[v]
        current_y = rest_y[v]

        # 既に到着したレストランは候補から削除
        candidates.pop(min_index)

    # 行かなきゃいけない配達先（＝これまでに行ったレストラン）のリスト
    candidates = orders.copy()

    # 今いる場所に最も近い配達先を貪欲に回る
    for _ in range(PICKUP_COUNT):
        # まだ行っていない配達先の中から、一番近い配達先を探す
        min_dist = 1000000007
        min_index = 998244353

        for i, v in enumerate(candidates):
            d = dist(current_x, current_y, dest_x[v], dest_y[v])
            if d < min_dist:
                min_dist = d
                min_index = i

        # 配達先の注文番号
        v = candidates[min_index]

        # 解を更新
        result_x.append(dest_x[v])
        result_y.append(dest_y[v])

        # 現在位置を更新
        current_x = dest_x[v]
        current_y = dest_y[v]

        # 既に到着した配達先は候補から削除
        candidates.pop(min_index)

    # 最後にオフィスに戻る
    result_x.append(CENTER)
    result_y.append(CENTER)

    return orders, result_x, result_y

かなり単純なアルゴリズムですが、それなりにうまく行きます。実はこれはNearest Neighbor法といって、れっきとした巡回セールスマン問題の解法の一つです。このコードを提出すると、1,115,375点で参加者549人中334位相当になります。この時点で既に水perf（β）です！

atcoder.jp

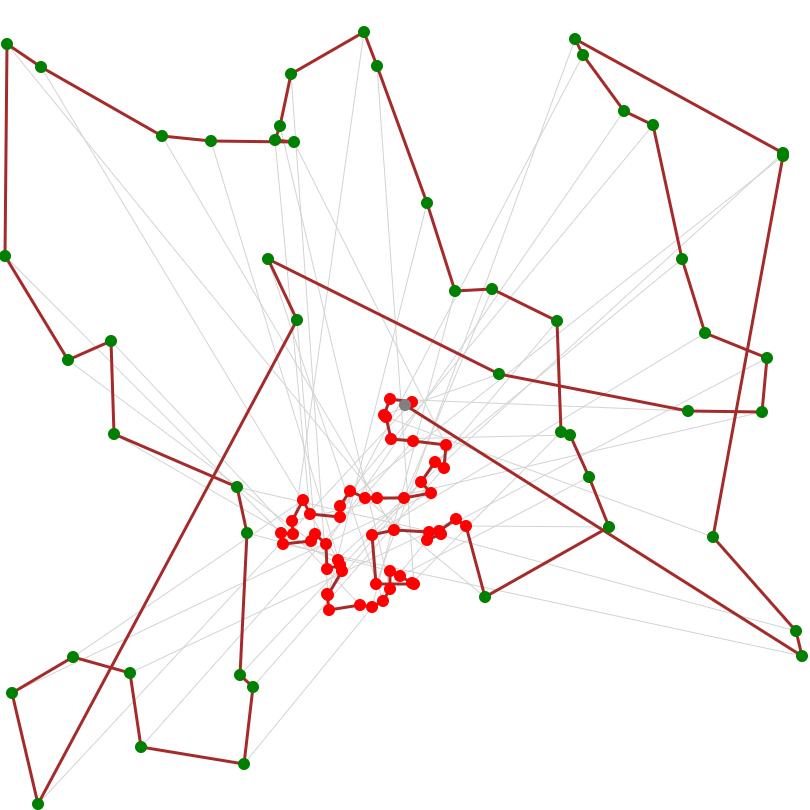
ビジュアライザはこんな感じです。人間が見ても理解できるような配達ルートになってきました。

f:id:terry_u16:20211125000741p:plain — ビジュアライザ (seed=0)

貪欲を改善する

もう一度ビジュアライザを見てみると、近くにあるレストランを優先した結果、配達先が遠くなっていることが分かります。ここからの改善方法は色々と考えられますが、とりあえずオフィスから遠すぎるレストラン・配達先は無視することにします。これで地の果てまで配達しなくても済むようになるでしょう。

以下のようなアルゴリズムになります。

高橋君は最初オフィスにいます。
オフィスからレストラン・配達先までのマンハッタン距離がともに閾値（今回は適当に400とします）以内の注文だけを列挙し、受ける注文の候補とします。
訪問したレストランが50軒に達するまで、今いる場所から一番近いレストランに移動することを繰り返します。
受けた注文を捌ききるまで、今いる場所から一番近い配達先に移動することを繰り返します。
オフィスに帰ります。

コードはこんな感じです。最初に注文の候補の列挙を追加しただけです。

def solve(rest_x, rest_y, dest_x, dest_y):
    """
    今いる場所に最も近いレストランを50個貪欲に回り、
    その後最も近い配達先を貪欲に回る
    ただし、候補はオフィスから距離400以下の場所のみとする
    """
    orders = []
    result_x = [CENTER]
    result_y = [CENTER]
 
    # [NEW!] 距離の閾値
    DEST_MAX = 400
 
    # 採用する注文の候補
    candidates = []
 
    # [NEW!] オフィスからの距離が閾値以内の注文のみを候補とする
    for i in range(ORDER_COUNT):
        dist_rest = dist(CENTER, CENTER, rest_x[i], rest_y[i])
        dist_dest = dist(CENTER, CENTER, dest_x[i], dest_y[i])
        if dist_rest <= DEST_MAX and dist_dest <= DEST_MAX:
            candidates.append(i)
 
    current_x = CENTER
    current_y = CENTER
 
    # 今いる場所に最も近いレストランを50個貪欲に回る
    for _ in range(PICKUP_COUNT):
        min_dist = 1000000007
        min_index = 998244353
 
        for i, v in enumerate(candidates):
            d = dist(current_x, current_y, rest_x[v], rest_y[v])
            if d < min_dist:
                min_dist = d
                min_index = i
 
        v = candidates[min_index]
        orders.append(v)
        result_x.append(rest_x[v])
        result_y.append(rest_y[v])
        current_x = rest_x[v]
        current_y = rest_y[v]
        candidates.pop(min_index)
 
    # 行かなきゃいけない配達先（＝これまでに行ったレストラン）のリスト
    candidates = orders.copy()
 
    # 今いる場所に最も近い配達先を貪欲に回る
    for _ in range(PICKUP_COUNT):
        min_dist = 1000000007
        min_index = 998244353
 
        for i, v in enumerate(candidates):
            d = dist(current_x, current_y, dest_x[v], dest_y[v])
            if d < min_dist:
                min_dist = d
                min_index = i
 
        v = candidates[min_index]
        result_x.append(dest_x[v])
        result_y.append(dest_y[v])
        current_x = dest_x[v]
        current_y = dest_y[v]
        candidates.pop(min_index)
 
    # 最後にオフィスに戻る
    result_x.append(CENTER)
    result_y.append(CENTER)
 
    return orders, result_x, result_y

これを提出すると、1,311,959点で参加者549人中259位相当になります。順位表の半分まで来ました！だいたい水perf上位（β）くらいになるみたいです。

atcoder.jp

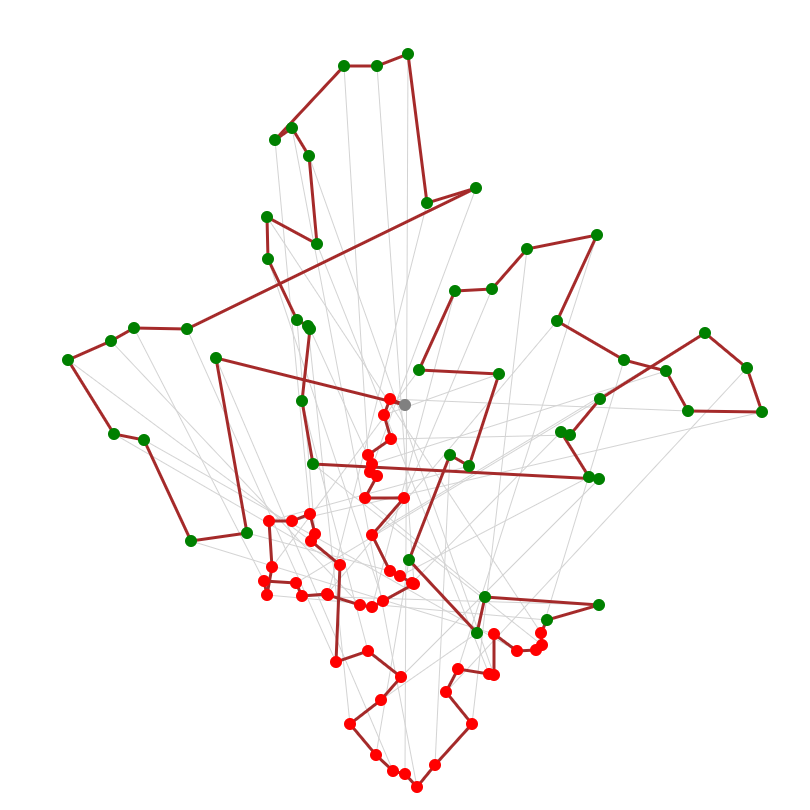
ビジュアライザはこちら。地の果てまで配達しなくてもよくなりました！

f:id:terry_u16:20211125002555p:plain — ビジュアライザ (seed=0)

制約を取り払う

ビジュアライザを見てみると、レストランを全部回りきる前に配達先に寄り道した方が良さそうに見えます。今まではレストランを50軒回ってから配達先を50軒回ることにしていましたが、この制約を取り払って $i$ 番目のレストランを訪れた後は $i$ 番目の配達先に行っても良いことにしましょう。

以下のようなアルゴリズムになります。

高橋君は最初オフィスにいます。
オフィスからレストラン・配達先までのマンハッタン距離がともに閾値（今回は適当に400とします）以内の注文だけを列挙し、受ける注文の候補とします。
今いる場所から一番近いレストランか配達先に移動することを繰り返します。回るレストラン・配達先はそれぞれ50軒までとします。
オフィスに帰ります。

コードにすると以下のようになります。今まではレストランのfor文と配達先のfor文を分けていましたが、今回一つにまとめました。

def solve(rest_x, rest_y, dest_x, dest_y):
    """
    今いる場所に最も近いレストランまたは配達先を貪欲に回る
    ただし、候補はオフィスから距離400以下の場所のみとする
    """
    orders = []
    result_x = [CENTER]
    result_y = [CENTER]
 
    # 距離の閾値
    DEST_MAX = 400
 
    # 採用する注文の候補
    candidates_rest = []
    candidates_dest = []
 
    for i in range(ORDER_COUNT):
        dist_rest = dist(CENTER, CENTER, rest_x[i], rest_y[i])
        dist_dest = dist(CENTER, CENTER, dest_x[i], dest_y[i])
        if dist_rest <= DEST_MAX and dist_dest <= DEST_MAX:
            candidates_rest.append(i)
 
    current_x = CENTER
    current_y = CENTER
 
    # [NEW!] 今いる場所に最も近いレストランまたは配達先を貪欲に回る
    for _ in range(PICKUP_COUNT * 2):
        min_dist = 1000000007
        min_index = 998244353
        is_restaurant = True
 
        # レストランを探索
        for i, v in enumerate(candidates_rest):
            d = dist(current_x, current_y, rest_x[v], rest_y[v])
            if d < min_dist:
                min_dist = d
                min_index = i
                is_restaurant = True
 
        # 配達先を探索
        for i, v in enumerate(candidates_dest):
            d = dist(current_x, current_y, dest_x[v], dest_y[v])
            if d < min_dist:
                min_dist = d
                min_index = i
                is_restaurant = False
 
        if is_restaurant:
            # レストランに行く場合
            v = candidates_rest[min_index]
            x = rest_x[v]
            y = rest_y[v]
            orders.append(v)
            candidates_dest.append(v)
            if len(orders) >= PICKUP_COUNT:
                # 50個になったらそれ以上レストランを探さない
                candidates_rest.clear()
            else:
                candidates_rest.pop(min_index)
        else:
            # 配達先に行く場合
            v = candidates_dest[min_index]
            x = dest_x[v]
            y = dest_y[v]
            candidates_dest.pop(min_index)
 
        result_x.append(x)
        result_y.append(y)
        current_x = x
        current_y = y
 
    # 最後にオフィスに戻る
    result_x.append(CENTER)
    result_y.append(CENTER)
 
    return orders, result_x, result_y

これを提出するとちょっと伸びて、1,347,640点で参加者549人中245位相当になります。

atcoder.jp

ビジュアライザはこちら。途中で少しだけ配達先に寄り道しているのが確認できます。

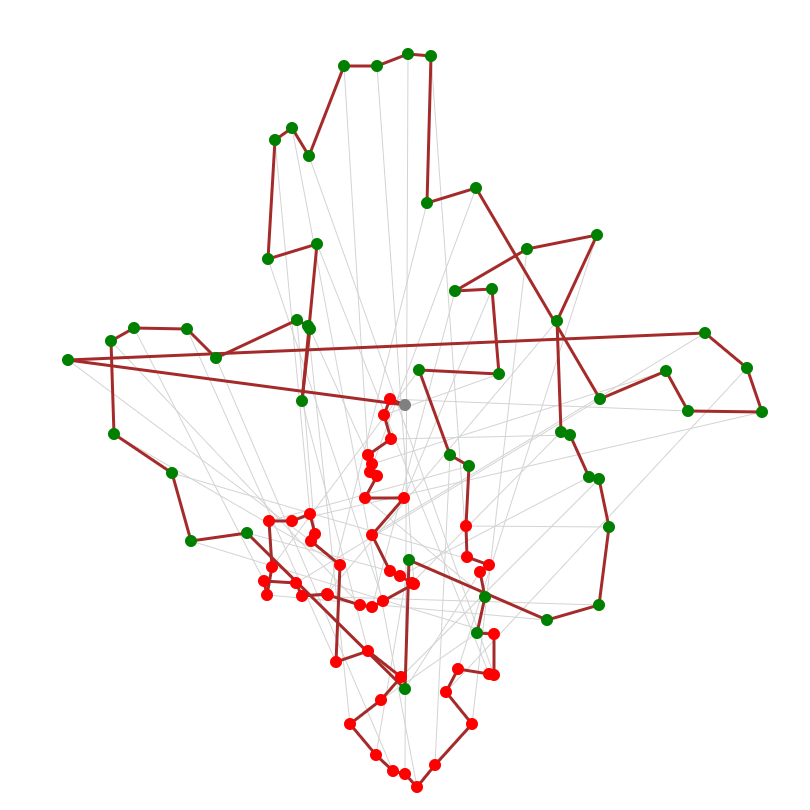
f:id:terry_u16:20211125004610p:plain — ビジュアライザ (seed=0)

アルゴの知識で改善する

今までは適当にオフィスからの距離が400までの注文を対象にしていましたが、もっとギリギリを攻められないでしょうか？何かABCで学んだアルゴリズムを使って……。

一旦ABCの問題文っぽく？書き直してみます。

2次元平面上の赤い点と緑の点のペアが $N$ 組与えられます。 $i$ 番目のペアにおける赤い点の座標は $(a_i, b_i)$ 、緑の点の座標は $(c_i, d_i)$ です。基準点 $(C, C)$ が与えられたとき、 $\max(|a_i-C|+|b_i-C|, |c_i-C|+|d_i-C|)\le D$ が成り立つような $i$ が $m$ 個以上となるような最小の $D$ を求めてください。

ざっくり茶diff～緑diffくらいでしょうか？どのようなアルゴリズムで解けるか、ちょっと考えてみてください。

▶クリックして解説を見る

基準点から距離 $D$ 以内にある点の個数には単調性があるので、二分探索を使うとよいです。まあ線形探索でもたぶん実行時間制限に間に合うんですが、せっかくなので二分探索を使うことにしましょう。*3

コードは以下のようになります。二分探索パートが追加されています。

def solve(rest_x, rest_y, dest_x, dest_y):
    """
    今いる場所に最も近いレストランまたは配達先を貪欲に回る
    ただし、候補はオフィスに近い場所のみとする
    オフィスからの距離の閾値は二分探索で求める
    """
    orders = []
    result_x = [CENTER]
    result_y = [CENTER]
 
    # [NEW!] 距離の閾値を二分探索で決める
    ok = 1000
    ng = 0
 
    while abs(ok - ng) > 1:
        med = (ok + ng) // 2
        count = 0
        for i in range(ORDER_COUNT):
            dist_rest = dist(CENTER, CENTER, rest_x[i], rest_y[i])
            dist_dest = dist(CENTER, CENTER, dest_x[i], dest_y[i])
            if dist_rest <= med and dist_dest <= med:
                count += 1
        if count >= PICKUP_COUNT:
            ok = med
        else:
            ng = med
        
    dest_max = ok
 
    # 採用する注文の候補
    candidates_rest = []
    candidates_dest = []
 
    for i in range(ORDER_COUNT):
        dist_rest = dist(CENTER, CENTER, rest_x[i], rest_y[i])
        dist_dest = dist(CENTER, CENTER, dest_x[i], dest_y[i])
        if dist_rest <= dest_max and dist_dest <= dest_max:
            candidates_rest.append(i)
 
 
    current_x = CENTER
    current_y = CENTER
 
    # 今いる場所に最も近いレストランまたは配達先を貪欲に回る
    for _ in range(PICKUP_COUNT * 2):
        min_dist = 1000000007
        min_index = 998244353
        is_restaurant = True
 
        # レストランを探索
        for i, v in enumerate(candidates_rest):
            d = dist(current_x, current_y, rest_x[v], rest_y[v])
            if d < min_dist:
                min_dist = d
                min_index = i
                is_restaurant = True
 
        # 配達先を探索
        for i, v in enumerate(candidates_dest):
            d = dist(current_x, current_y, dest_x[v], dest_y[v])
            if d < min_dist:
                min_dist = d
                min_index = i
                is_restaurant = False
 
        if is_restaurant:
            # レストランに行く場合
            v = candidates_rest[min_index]
            x = rest_x[v]
            y = rest_y[v]
            orders.append(v)
            candidates_dest.append(v)
            if len(orders) >= PICKUP_COUNT:
                # 50個になったらそれ以上レストランを探さない
                candidates_rest.clear()
            else:
                candidates_rest.pop(min_index)
        else:
            # 配達先に行く場合
            v = candidates_dest[min_index]
            x = dest_x[v]
            y = dest_y[v]
            candidates_dest.pop(min_index)
 
        result_x.append(x)
        result_y.append(y)
        current_x = x
        current_y = y
 
    # 最後にオフィスに戻る
    result_x.append(CENTER)
    result_y.append(CENTER)
 
    return orders, result_x, result_y

これを提出すると、1,382,916点で参加者549人中225位相当になります。ここまでできると青perf（β）になるみたいですね。

atcoder.jp

ビジュアライザはこんな感じです。だいぶ小さくまとまりましたね。

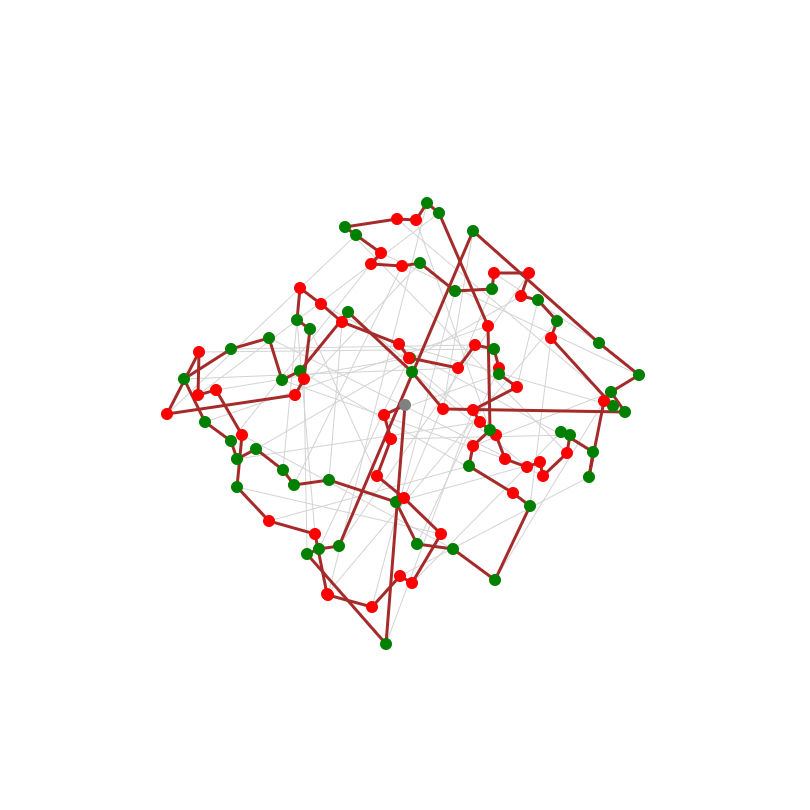
f:id:terry_u16:20211125011659p:plain — ビジュアライザ (seed=0)

貪欲その2

別の貪欲を試してみる

だんだんスコアの上昇幅が小さくなってきました。ちょっと方針転換しないと順位表2ページ目は厳しそうです。

もう一度ビジュアライザを見てみましょう。1個前のビジュアライズ結果は小さくまとまりすぎて見辛いので、2個前のものが考察しやすいかもしれません。

レストラン（赤）はかなりいい感じに回れているのですが、配達先（緑）があちこちに散らばってしまっています。これは、「どの注文を選ぶか？」を決める際に、レストランの近さだけで選択し、配達先の近さを無視してしまっているためです。レストランも配達先もできるだけ近くになるよう選ぶ方法はないのでしょうか？

あります。レストランだけ・配達先だけを1個ずつ追加していくのではなく、レストランと配達先のペアをまとめて追加していくと良さそうです。こうすることで、片方のためにもう片方が犠牲になることを防げます。

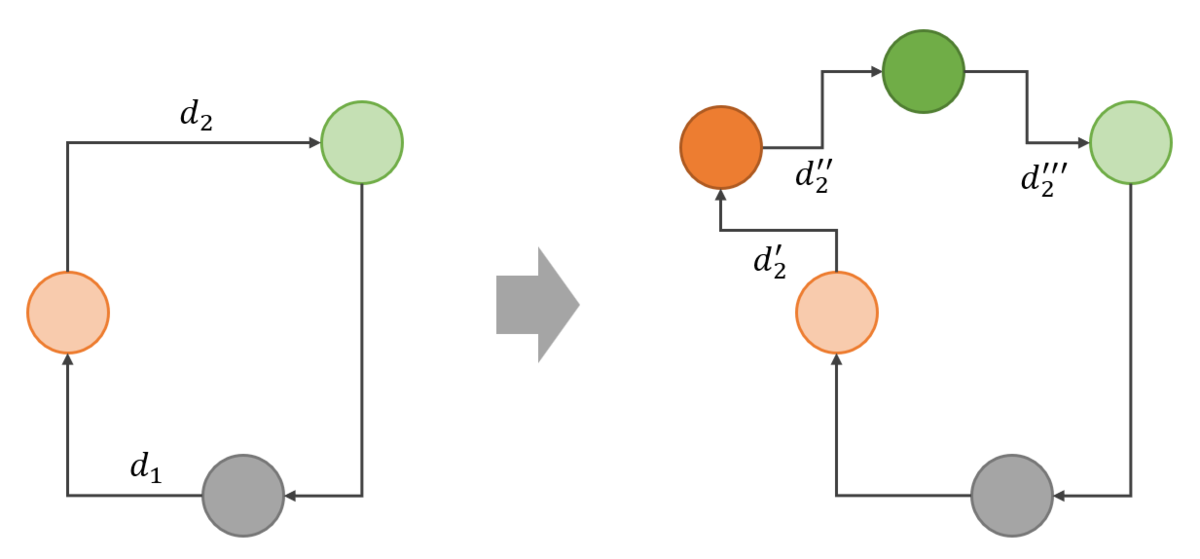
「今いる場所から最も近いペアを選ぶ」とするとあまり上手く行かないので、ちょっと考え方を変えてみます。「今の配達ルートから寄り道するときに、一番移動距離の増加が小さいペアを挿入する」という考え方で行ってみましょう。図にするとこんな感じです。

f:id:terry_u16:20211125204513p:plain — レストラン・配達先のペアの挿入

この時の移動距離の増加量は $(d_1'+d_1''-d_1)+(d_2'+d_2''-d_2)$ で求めることができます。これを全てのペア・全ての挿入場所について全探索して、移動距離の増加量が最も小さいものを貪欲に追加していきます。アルゴリズムをまとめると、以下のようになります。

オフィスから出て、何もせずにオフィスに帰るという配達ルートを設定します。移動距離は当然0です。
まだ選んでいない注文全てについて、レストラン・配達先の挿入場所を全探索し、最も移動距離の増加が小さい注文を選んで最適な位置に挿入します。
2.を50回繰り返し、最終的な解を得ます。

コードにすると以下のようになります。

def solve(rest_x, rest_y, dest_x, dest_y):
    """
    寄り道をしたときに、
    最も距離の増加が少ないレストラン・配達先のペアを50個選ぶ
    """
    orders = []
    result_x = [CENTER, CENTER]
    result_y = [CENTER, CENTER]
 
    # 採用する注文の候補
    candidates = list(range(ORDER_COUNT))
 
    # オーダーの追加を50回繰り返す
    for _ in range(PICKUP_COUNT):
        min_dist = 1000000007
        # (選んだインデックス, レストラン挿入先, 配達先挿入先)
        min_indice = 0, 0, 0
 
        # 各オーダーについて、最適なレストラン・配達先の挿入先(j, k)を全探索
        for i, v in enumerate(candidates):
            x0 = rest_x[v]
            y0 = rest_y[v]
            x1 = dest_x[v]
            y1 = dest_y[v]
 
            # レストランの挿入先を探す
            for j in range(1, len(result_x)):
                old_dist_rest = dist(result_x[j - 1], result_y[j - 1], result_x[j], result_y[j])
                d00 = dist(result_x[j - 1], result_y[j - 1], x0, y0)
                d01 = dist(x0, y0, result_x[j], result_y[j])
                new_dist_rest = d00 + d01
 
                # j番目にレストランを挿入したときの距離の差分
                dist_diff_rest = new_dist_rest - old_dist_rest
 
                # コーナーケースが面倒なので、一旦挿入する（後で削除）
                result_x.insert(j, x0)
                result_y.insert(j, y0)
 
                # 配達先の挿入先を探す
                for k in range(j + 1, len(result_x)):
                    old_dist_dest = dist(result_x[k - 1], result_y[k - 1], result_x[k], result_y[k])
                    d10 = dist(result_x[k - 1], result_y[k - 1], x1, y1)
                    d11 = dist(x1, y1, result_x[k], result_y[k])
                    new_dist_dest = d10 + d11
 
                    # k番目に配達先を挿入したときの距離の差分
                    dist_diff_dest = new_dist_dest - old_dist_dest
 
                    # (j, k)番目にそれぞれ挿入したときの距離の差分
                    dist_diff = dist_diff_rest + dist_diff_dest
 
                    # 最小値の更新
                    if dist_diff < min_dist:
                        min_dist = dist_diff
                        min_indice = i, j, k
 
                # 挿入していたやつを削除
                result_x.pop(j)
                result_y.pop(j)
 
        # オーダーの追加を行う
        i, j, k = min_indice
        v = candidates[i]
        orders.append(v)
        candidates.pop(i)
 
        # 寄り道するレストラン・配達先を挿入する
        # 挿入順を間違えるとインデックスがズレるので注意
        result_x.insert(j, rest_x[v])
        result_y.insert(j, rest_y[v])
        result_x.insert(k, dest_x[v])
        result_y.insert(k, dest_y[v])
 
    return orders, result_x, result_y

ビジュアライザを見てみましょう。なんだかかなりいい感じに見えます。配達先が遠くになってしまうこともなく、なおかつ二分探索のときのように同じ場所をぐるぐる回ったりもしてなさそうです。

f:id:terry_u16:20211125210052p:plain — ビジュアライザ (seed=0)

これを提出すると……？残念ながらTLEになってしまいます。実はこのアルゴリズムは $O(Nm^3)$ となっており、限界高速化でもしない限り実行時間に間に合わせるのは厳しそうです。

atcoder.jp

アルゴの知識で高速化する

ここでもABCで学んだアルゴリズムの知識が役に立ちます。計算量のオーダーを落としていきましょう。

問題文にするならこんな感じでしょうか。

2次元平面上の点列 $\left( (x_1, y_1), \cdots, (x_{2m-2}, y_{2m-2})\right)$ が与えられます。赤い点 $(a, b)$ と緑の点 $(c, d)$ をこの点列に挿入して、長さ $2m$ の点列を作ります。挿入後の赤い点のインデックスを $i$ 、緑の点のインデックスを $j$ として、 $i\lt j$ が成り立つように挿入するとき、 $\sum_{k=1}^{2m-1} {\left(|x_{k+1}-x_k|+|{y_{k+1}-y_k}|\right)}$ が最小になるような $i, j$ を求めてください。

$i, j$ を全探索すれば $O(m^2)$ で解けます*4が、 $O(m)$ で解いてみてください。緑diffくらいでしょうか？

▶クリックして解説を見る

緑の点を $j$ 番目に挿入するとき、赤い点の挿入位置は $1, 2, \cdots, j-1$ 番目から選べます。赤い点の挿入位置を $1, 2, \cdots, j-1$ 番目から選んだときの距離の増加量の最小値を前計算しておけば、各 $j$ について $O(1)$ で最適な $i$ を求めることができます。赤い点の挿入位置を $1, 2, \cdots, j-1$ 番目から選んだときの最小値は累積minを行うことで $O(m)$ で計算できるので、 $O(m)$ で解くことができそうです。

このアルゴリズムを先ほどのコードに盛り込むことで、 $O(Nm^3)$ から $O(Nm^2)$ に計算量を落とすことができます。下図のように、赤い点と緑の点を隣接して挿入するコーナーケースに注意してください（距離の増加量は $(d_2'+d_2''+d_2'''-d_2)$ になります）。

f:id:terry_u16:20211125220310p:plain — 隣接して挿入するケース

def solve(rest_x, rest_y, dest_x, dest_y):
    """
    寄り道をしたときに、
    最も距離の増加が少ないレストラン・配達先のペアを50個選ぶ
    """
    orders = []
    result_x = [CENTER, CENTER]
    result_y = [CENTER, CENTER]

    # 採用する注文の候補
    candidates = list(range(ORDER_COUNT))

    # オーダーの追加を50回繰り返す
    for _ in range(PICKUP_COUNT):
        min_dist = 1000000007
        # (選んだインデックス, レストラン挿入先, 配達先挿入先)
        min_indice = 0, 0, 0

        # l番目までを見たときの、最適なレストランの挿入位置を求めるための配列
        min_rest_dist = [1000000007] * len(result_x)
        min_rest_index = [998244353] * len(result_x)

        # 各オーダーについて、最適なレストラン・配達先の挿入先(j, k)を全探索
        for i, v in enumerate(candidates):
            x0 = rest_x[v]
            y0 = rest_y[v]
            x1 = dest_x[v]
            y1 = dest_y[v]

            min_rest_dist[0] = 1000000007

            # j番目までを見たときの、最適なレストランの挿入位置を求めておく
            for j in range(1, len(result_x)):
                prev_x = result_x[j - 1]
                prev_y = result_y[j - 1]
                next_x = result_x[j]
                next_y = result_y[j]

                old_dist_rest = dist(prev_x, prev_y, next_x, next_y)
                d00 = dist(prev_x, prev_y, x0, y0)
                d01 = dist(x0, y0, next_x, next_y)
                new_dist_rest = d00 + d01

                # j番目にレストランを挿入したときの距離の差分
                min_rest_dist[j] = new_dist_rest - old_dist_rest

                # 先頭から累積minを取っておく
                if min_rest_dist[j] < min_rest_dist[j - 1]:
                    min_rest_index[j] = j
                else:
                    min_rest_dist[j] = min_rest_dist[j - 1]
                    min_rest_index[j] = min_rest_index[j - 1]

            # 配達先の挿入先を探す
            for k in range(1, len(result_x)):
                prev_x = result_x[k - 1]
                prev_y = result_y[k - 1]
                next_x = result_x[k]
                next_y = result_y[k]

                # k - 1番目までにレストランを挿入したときの距離の差分
                dist_diff_rest = min_rest_dist[k - 1]

                old_dist_dest = dist(prev_x, prev_y, next_x, next_y)
                d10 = dist(prev_x, prev_y, x1, y1)
                d11 = dist(x1, y1, next_x, next_y)
                new_dist_dest = d10 + d11

                # k番目に配達先を挿入したときの距離の差分
                dist_diff_dest = new_dist_dest - old_dist_dest

                # (j, k)番目にそれぞれ挿入したときの距離の差分
                dist_diff = dist_diff_rest + dist_diff_dest

                # 最小値の更新
                if dist_diff < min_dist:
                    min_dist = dist_diff
                    # jを先に挿入するとkのインデックスが1つずれることに注意
                    min_indice = i, min_rest_index[k], k + 1

                # k番目にレストランと配達先を両方入れるケースもあるので、
                # この場合は場合分けが必要
                old_dist = dist(prev_x, prev_y, next_x, next_y)
                d10 = dist(prev_x, prev_y, x0, y0)
                d11 = dist(x0, y0, x1, y1)
                d12 = dist(x1, y1, next_x, next_y)
                new_dist = d10 + d11 + d12

                # (k, k)番目にそれぞれ挿入したときの距離の差分
                dist_diff = new_dist - old_dist

                # 最小値の更新
                if dist_diff < min_dist:
                    min_dist = dist_diff
                    # jを先に挿入するとkのインデックスが1つずれることに注意
                    min_indice = i, k, k + 1

        # オーダーの追加を行う
        i, j, k = min_indice
        v = candidates[i]
        orders.append(v)
        candidates.pop(i)

        # 寄り道する座標を挿入する。順番に注意
        result_x.insert(j, rest_x[v])
        result_y.insert(j, rest_y[v])
        result_x.insert(k, dest_x[v])
        result_y.insert(k, dest_y[v])

    return orders, result_x, result_y

ビジュアライザを見てみましょう。先ほどと同じ結果が得られていることが確認できます。

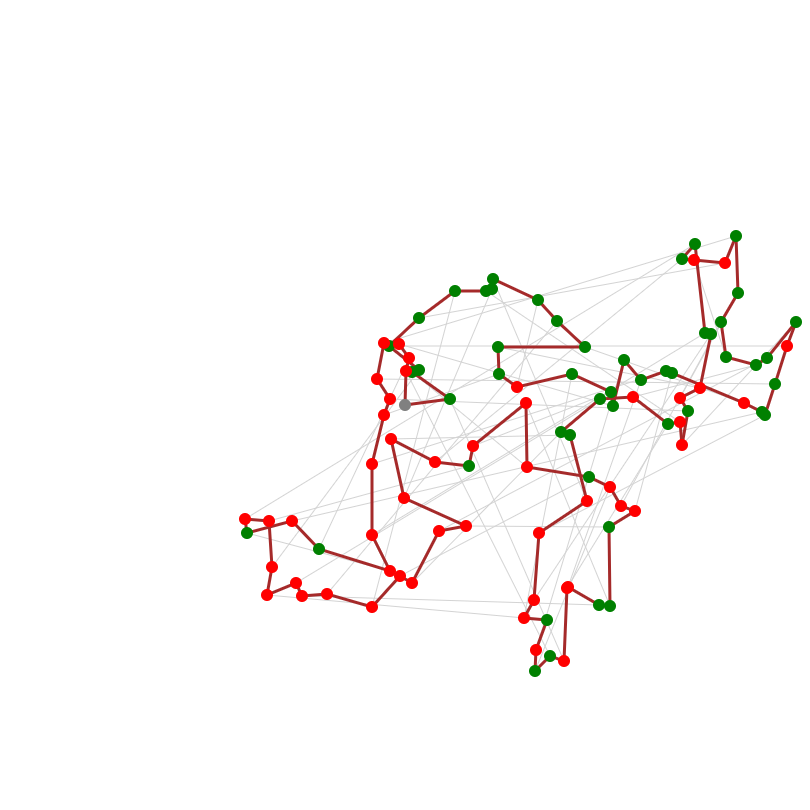
f:id:terry_u16:20211125014449p:plain — ビジュアライザ (seed=0)

ちなみに挿入の様子を動画にするとこんな感じです。ちょっとずつ配達ルートが成長していって面白いですね。

f:id:terry_u16:20211126205552g:plain — ビジュアライザ（動画版）

これを提出すると、1,829,903点が得られました。*5参加者549人中37位相当の得点で、見事順位表2ページ目に入ることができました！これはなんと橙perf（β）相当の成績です。もちろんここから工夫次第でさらにスコアを上げることもできるでしょう。

atcoder.jp

おわりに

いかがでしたでしょうか？焼きなましやビームサーチを使わず、貪欲だけで無事順位表2ページ目に入ることができました。その貪欲というのも天才的な貪欲ではなく、「できるだけ近いところに寄り道する」という方針で、割と人間の直感に合った解法だったのではないかと思います。*6

また、今回はビジュアライザを何度も見て、そこから改善できそうな点を探しました。ビジュアライザを見ると改善できそうな点が結構見付かるので、積極的に活用することをおすすめします。

というわけで、貪欲だけでも十分、いや十二分に戦うことができます！「焼きなましとか知らないから……」と躊躇せず、是非とも直感に頼った貪欲でAHCに参加してみてください！この記事をきっかけに、ヒューリスティックコンテストに参加される方が少しでも増えたら嬉しく思います。

*1:色が見辛い方はごめんなさい……。

*2:このように、実装が大変そうならサボるのもアリです。とりあえず動くものを作って、少しずつ改善していきましょう。

*3:別解として、オフィスからの距離でソートしてもよいです。

*4:点を挿入したときのマンハッタン距離の増加量はO(1)で求められます。

*5:実行時間が危なかったので内心ヒヤヒヤしていました。企画倒れにならなくてよかったです……。

*6:振り返ってみればシンプルな解法ですが、短時間のコンテスト中にここに辿り着くのはなかなか難しいです。だからこそ橙perf相当になったわけで。

TERRYのブログ

最近は競技プログラミングにお熱。

AHC006初心者向け解説～貪欲だけで順位表2ページ目を目指す～

伝えたいことを3行で

対象読者

問題概要

テンプレコード

貪欲その1

とりあえず貪欲をする

貪欲を改善する

制約を取り払う

アルゴの知識で改善する

貪欲その2

別の貪欲を試してみる

アルゴの知識で高速化する

おわりに