TERRYのブログ

最近は競技プログラミングにお熱。

Sponsored Link

トップ > 競プロ > 2人同時着手ゲームでモンテカルロ木探索を使う（Decoupled UCT）

2人同時着手ゲームでモンテカルロ木探索を使う（Decoupled UCT）

競プロ ゲームAI マラソン

2023/02/17追記

上位互換の本が出ました！皆様こちらを買いましょう。

ゲームで学ぶ探索アルゴリズム実践入門～木探索とメタヒューリスティクス

ゲームで学ぶ探索アルゴリズム実践入門～木探索とメタヒューリスティクス

Amazon

はじめに

CodingameのSpring Challenge 2021にて、モンテカルロ木探索が使えるゲームが出題されました。

2人同時着手ゲーム向けのモンテカルロ木探索はDUCT (Decoupled Upper Confidence Tree) というものを使うのですが、日本語のまとまった解説記事がほとんどなさそうなので書いてみます。

前提知識として、普通のモンテカルロ木探索については知っていると仮定して書きます。モンテカルロ木探索が分からないという方は他の方の解説記事や書籍を読んで頂ければ幸いです。なお、普通のモンテカルロ木探索の実装方法が分からないという方にはこちらの書籍がオススメです。*1

AlphaZero 深層学習・強化学習・探索 人工知能プログラミング実践入門

AlphaZero 深層学習・強化学習・探索 人工知能プログラミング実践入門

Amazon

DUCTの必要性

そもそもなぜ普通のモンテカルロ木探索じゃダメなの？というところから。

普通のモンテカルロ木探索は（自分）→（相手）→（自分）→……といった流れで交互にノードを展開していきます。これを同時着手ゲームに適用すると、以下のような問題が発生します。

  • 相手は自分の出方を見てから着手できるため、後出しじゃんけん状態になってしまう。
  • 自分と相手でリソースを共有している場合、自分がリソースを不当に自由に使えてしまう。

これを解消するため、じゃあ自分と相手で同時に手を選択させればいいんじゃね？というのがDUCTです。発想としては自然かなと思います。

なお、同時着手ゲームならDUCTの方が絶対強いかというとそうとも断言出来なさそうで、例えばこちらの論文ではTronというゲームに適用した場合、ナイーブなモンテカルロ木探索とDUCTでほぼ互角～やや不利だったことが報告されています。*2

DUCTのアルゴリズム

以下のようなシチュエーションを考えてみましょう。

  • 自分はA～Dの4つの選択肢、相手はX～Zの3つの選択肢が選べる
  • 既に10回プレイアウト済み

普通のモンテカルロ木探索はSelection→Expansion→Evaluation→Backupという流れで処理を行っていくので、今回もそれに倣って解説していきます。

Selection

まず、自分と相手について、それぞれ独立に各選択肢の試行回数と累計報酬を持たせておきます。普通のモンテカルロ木探索のテーブルが2つになっただけですね。

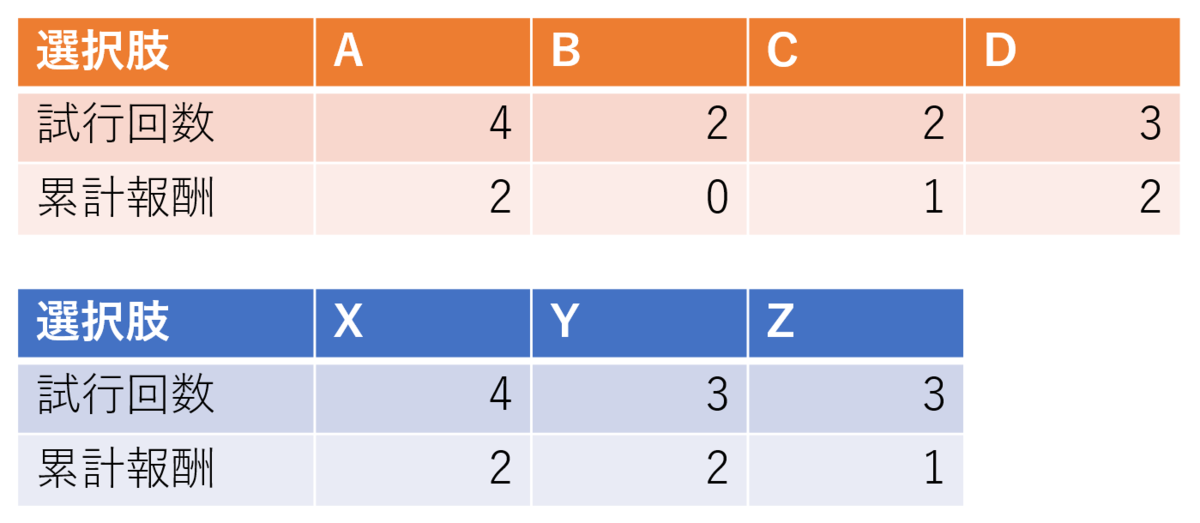
それぞれ独立にUCB1を計算し、UCB1の一番大きかった手を選びます。何のことはなく、普通のモンテカルロ木探索の処理を2回やっているだけです。

2人の手が決まったら、そのペア(C, Y)を1つの手として考え、子ノードに移ります。実装上は子ノードを2次元配列として持っておくとよいです。

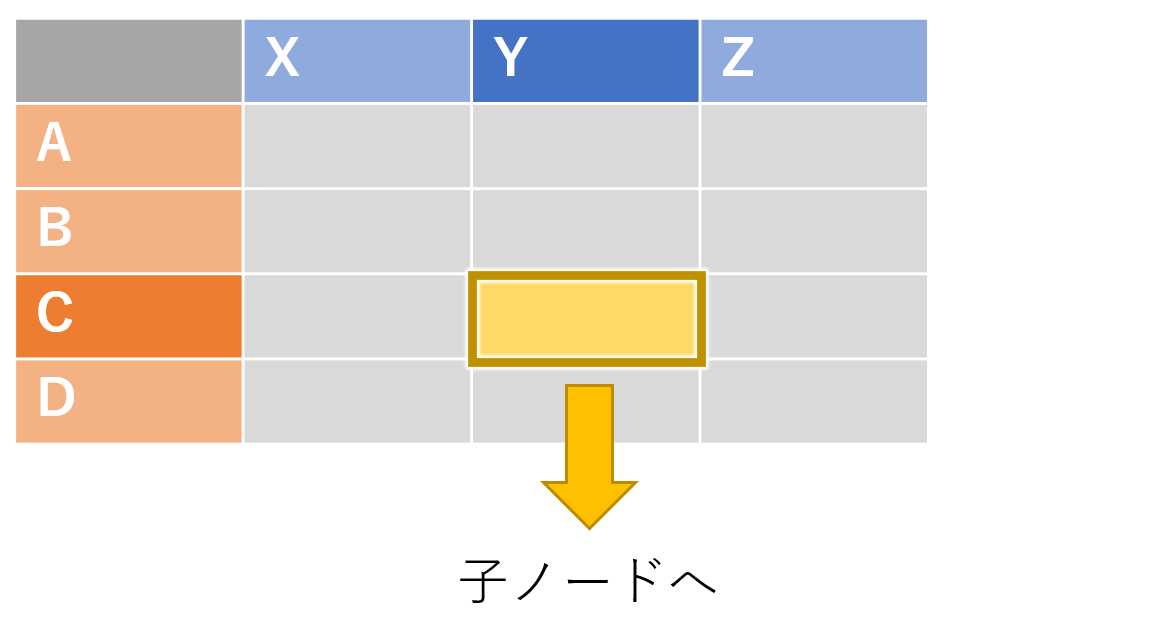
Expansion

普通のモンテカルロ木探索と同じです。子ノードが未展開で、かつ訪れた回数が閾値に達したら、ノードを展開します。

Evalutaion

これも普通のモンテカルロ木探索と同じです。葉ノードまで到達したら、普通のモンテカルロ木探索と同様にプレイアウトして報酬を得ます。別にプレイアウトじゃなくて評価関数で決めても良いです。

Backup

報酬が決まったら、各ノードについて試行回数と累計報酬を更新します。これも普通のモンテカルロ木探索の処理を2回やっているだけです。

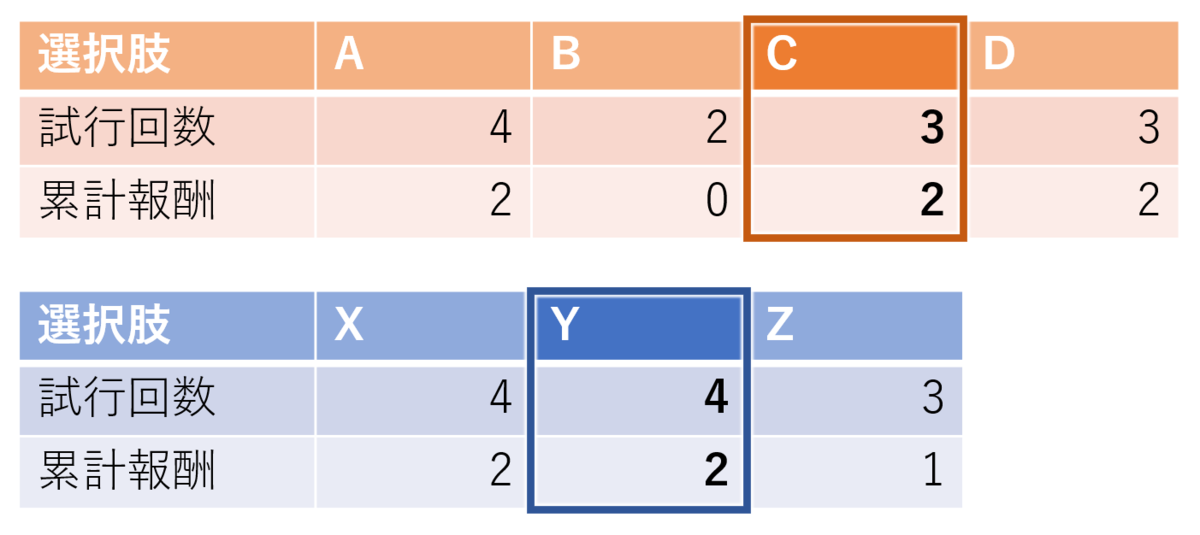
終わりです。簡単でしょ？

Play

あとはこれを時間いっぱい繰り返して、自分が一番多く選んだ手をA～Dの中から選んで出力すればよいです。DUCT (mix) なる選び方もあるらしいですが、よく分からないので説明しません。言うほど強くないっぽいし……。

メリットとデメリット

DUCTを採用するメリットは以下です。ナイーブなモンテカルロ木探索の欠点の裏返しですね。

  1. 後出しじゃんけん状態が発生しない
  2. リソースを不当に自由に使えてしまう問題も起こらない

逆にデメリットは以下です。

  1. 子ノードが多いため収束性が悪く、深く読むことが難しい
  2. 子ノードを2次元配列で持つため、若干メモリを食う（諸説あり）

特に1.が痛いです。自分の選択肢がn個、相手の選択肢がm個ある場合、子ノードの数はnm個となるため、なかなかノードの展開が行われないことが多いです。弱い選択肢の枝刈りなどを行うと2乗で効いてくるので、積極的に枝刈りしていくとよいと思います。*3

また、3人以上のゲームに適用すると子ノード数が指数関数的に増えていくため、よほど選択肢が少ないゲームでない限りあまり現実的ではない気がします。Tron Battleくらいのシンプルなゲーム（選択肢が3^4=81通り）くらいならいけるかもしれませんが、試していないのでよく分からず……。

UCB1-Tunedを使う

おまけです。

これはDUCTに限らず普通のモンテカルロ木探索にも言えることなのですが、UCB1の代わりにUCB1-Tunedを使うと性能が上がることがあります。*4UCB1-Tunedは報酬の分散も考慮した式で、理論的保証はないですが多腕バンディット問題においてUCB1より優れた結果を出すとのことです。ハズレばっかり出す選択肢は見込みがないけど、外れたり当たったりする選択肢はもうちょっと調べてみよう、みたいなお気持ちなんだと思います。

UCB1-Tunedは以下の式より得られます。

\mathrm{UCB1tuned} _i=\frac {v_i} {n_i} + \sqrt{\frac{\min(1/4, \mathrm{Var}_i) \ln N}{n_i}}

\mathrm{Var}_i=\sigma_i^2+\sqrt \frac{2\ln N}{n_i}

ここで、

N：全ての子ノードの試行回数の合計
v_i：子ノードiの累計報酬
n_i：子ノードiの試行回数
\sigma_i^2：子ノードiの報酬の分散

です。ちなみに分散 \sigma^2は、

\sigma^2=\frac 1 n \sum_{j=1}^{n} {v_j^2}-(\frac 1 n \sum_{j=1}^{n} {v_j})^2

のように（2乗の平均）ー（平均の2乗）の形で書けるので、差分計算が可能です。

こちらの論文では、UCB1からUCB1-Tunedに変更した場合、ナイーブなモンテカルロ木探索よりもDUCTの方が性能の上がり幅が大きかったことが報告されています。これは推測なのですが、おそらくDUCTは子ノードが多いため、UCB1-Tunedに変更することによる収束性の向上の恩恵が大きかったのではないかと考えています。

UCB1-Tuned以外にも、多腕バンディット問題の探索ポリシーとして様々な式が考案されているので、色々試してみるのもよいかもしれません。

まとめ

まとめると、DUCTとナイーブなモンテカルロ木探索の違いは、

  • 2人同時に着手する
  • 1つのノードに試行回数と累計報酬のテーブルを2つ持つ（自分用と相手用）
  • 自分と相手の行動のペアを1つの行動として考える

くらいで、あとはほぼ同じです。モンテカルロ木探索さえ書ければ移行もそんなに難しくないので、一度試してみてはいかがでしょうか。

*1:こちらの書籍は出版社のサイトからpdf版も購入できるのですが、その場合ぼくにアフィリエイトの紹介料が入らないので、ぜひ紙の本を買ってください。ちなみに当ブログですが、びっくりするほど赤字垂れ流しです。

*2:ただし、後述のUCB1-Tunedに変更したDUCTは、同じくUCB1-Tunedに変更した普通のモンテカルロ木探索より強くなっています。

*3:Codingame Spring Challenge 2021では、Seedの選択肢を削ったらかなり強くなりました。

*4:必ず上がるとは言えません。特にシンプルなゲームだと計算量の増大によるプレイアウト数減少のデメリットの方が大きいかもしれません。