AHC018お疲れ様でした。相対スコア2,165,296,633,344点で36位でした。

ガウス過程という概念を新しく学んだので、自分への備忘も兼ねて解説を書きます。

問題概要
方針
前提知識
- ガウス過程
- 最小シュタイナー木問題
解法
おまけ: CNN解法
日記
感想

問題概要

水源から家までできるだけ省エネで水を引いてね。

岩盤の頑丈さは壊してみるまで分からないよ。

atcoder.jp

方針

久々に不完全情報ゲー（？）が来ましたね。AtCoderだと2021年のHTTF予選以来でしょうか。

方針としては、経路上の点をいくつか試し掘りすることを繰り返して経路を決めて、その後本格的に掘り進めるという流れとしました。

岩盤の頑丈さを何かしらの手法で予測できると無駄なパワーを使わなくて良さそうなので、ガウス過程を使って頑丈さを推定することにしました。ガウス過程を使うと、頑丈さの推定値に加えてどのくらい推定値に自信があるかという情報も得ることができるので、自信がないところを積極的に試し掘りすることでより良い経路を見付けられる可能性が高まります。一方で試し掘りを無限にするわけにも行かないので、バランスが難しいです。探索と活用というやつですね。

前提知識

今回の解法は事前に必要な知識が多めです。

ガウス過程

私も最近勉強したばかり*1なので理解が怪しいのですが、ざっと説明します。理論面はすっ飛ばして、何が嬉しいかという点に絞って書いていきます。変なこと言ってたらご指摘ください……。

サイコロを投げると1〜6の数字がランダムに出てきます。言い方を変えると、サイコロとは1回使うとあるルールに従った何かしらのランダムな値を返してくる装置と見ることができます。ガウス過程はそれと同じように、1回使うとあるルールに従った何かしらのランダムな関数 $f(\boldsymbol{x})$ を返してくれる装置と思うと良いらしいです。今回の問題の場合、関数とはある座標 $(x, y)$ における頑丈さ $S(x,y)$ を指していると思ってください。ボタンを押すたびになんかそれっぽいランダムな頑丈さのマップが出てくる、そんなイメージです。

で、ランダムな関数といってもあらゆる関数 $f(\boldsymbol{x})$ が等確率で出てくるわけではなく、出やすい関数の形・出にくい関数の形というものが存在します。今回の問題でも、頑丈さ10のマスの隣が頑丈さ5000になっているとか、全部のマスが頑丈さ5000になっているとか、そういった関数は考えにくいですよね。ここでどんな関数が出やすいか・どんな関数が出にくいかというのはガウス過程という装置の特性によるのですが、試し掘りしたデータをもとにその特性を求めるのがガウス過程回帰です。

そういった考えられうるあらゆる関数を無限個集めると、「平均してこのくらいかな〜」というような頑丈さの期待値の関数 $\bar S(x,y)$ を考えることができます。そうすると「座標 $(x,y)$ は頑丈さの期待値が500くらいだから、パワー10ずつちまちま掘らずに一気に400くらい掘っちゃっても良いかな」みたいなことが分かって、効率的に掘れるようになります。しかも勘ではなく数学の後ろ盾付きで。これは嬉しいですね。

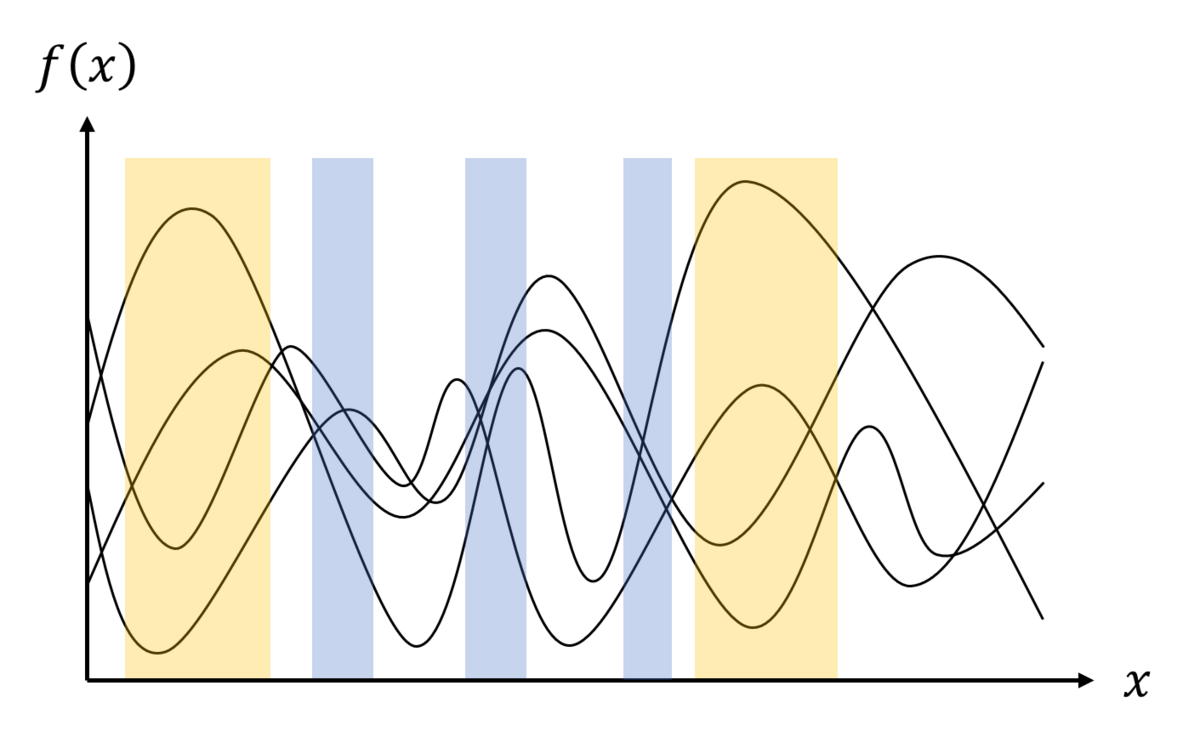
それに加えて、「この座標 $(x,y)$ のあたりはどの関数も頑丈さ100前後で、頑丈さのばらつきが小さいな」「この座標 $(x', y')$ のあたりは頑丈さ200のものもあれば頑丈さ4000のものもあって、めちゃくちゃブレ幅が大きいな」ということが分かってきます。このブレ幅が小さいところは自信を持って頑丈さ100と言えますし、ブレ幅が大きいところは試し掘りしてみないと確かなことは言えない、ということまで判断できるようになります。なんだかとても嬉しい気持ちになってきませんか？

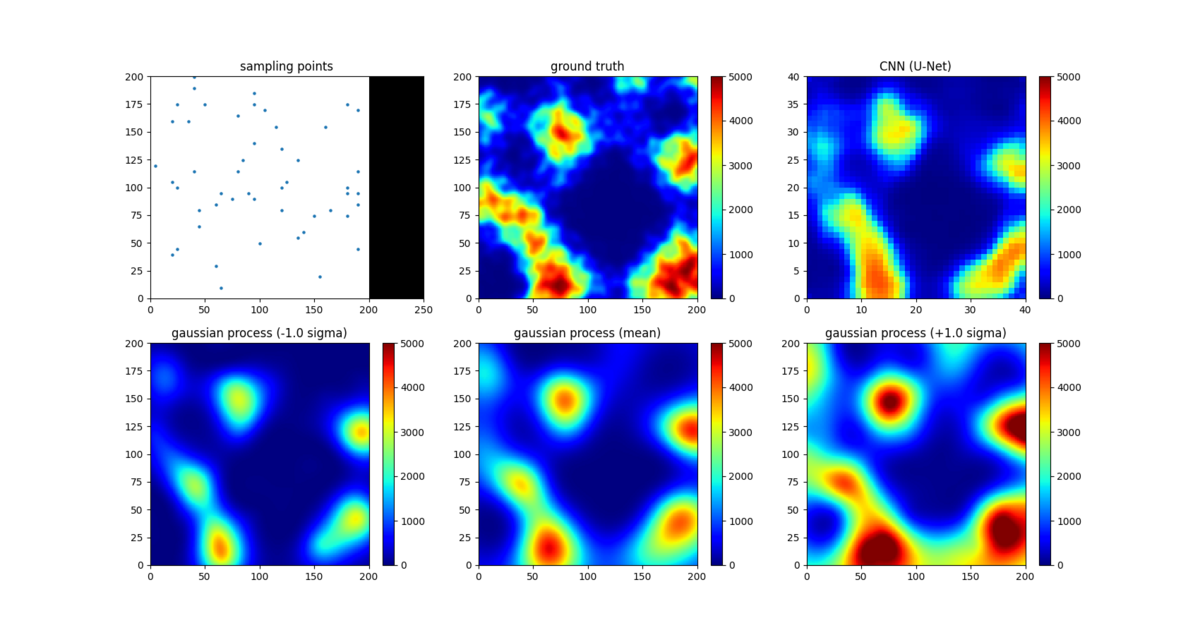
関数をランダムに4つ作ったときのイメージ。ばらつきが小さい箇所（青）と大きい箇所（黄）がある。青い箇所を試し掘りするより黄色い箇所を試し掘りした方が多くの情報を得られそうな気持ちになる。

という感じで、ガウス過程回帰を使うと「各座標の頑丈さの期待値がどれくらいか」「その値はどのくらいバラつくか」ということが分かるので、とても嬉しいです。実際に使ってみた図を貼っておきます。中央上が実際の頑丈さで、左上が試し掘りした点、そして中央下がガウス過程を使って求めた期待値です。なんか良い感じに期待値を推測できてそうです。また左下は頑丈さが下振れしたときの予測値、右下は頑丈さが上振れしたときの予測値になっています。図だと分かりづらいですが、点の少ないところほど上振れ・下振れのブレ幅が大きくなっています。*2

という感じでガウス過程を勉強すると嬉しいことがいっぱいです。正直理論としては難しい（大学の学部1〜2年レベルの線形代数と確率の知識は最低限必要だと思います）のですが、勉強してみたいという方には以下の本がとてもオススメです。

ガウス過程と機械学習 (機械学習プロフェッショナルシリーズ)

作者:持橋大地,大羽成征
講談社

Amazon

最小シュタイナー木問題

最小シュタイナー木問題の理解には最小全域木問題の知識が必要です。ご存じない方は調べて頂ければ。

最小シュタイナー木問題とは何かというと、「使っても使わなくてもどっちでもいい点が与えられる最小全域木問題」です。今回の問題の場合、水源と家が「必ず使わなければならない点」、それ以外のマスが「使っても使わなくてもどっちでもいい点」です。*3

最小全域木問題は、辺の本数を $E$ とするとクラスカル法やプリム法で $O(E\log E)$ で解くことができますが、最小シュタイナー木問題はNP困難であり、多項式時間で解く方法は見つかっていません。

ちなみに指数時間での比較的効率的な厳密解法はあって、wataさんのスライドが詳しいです。しかし今回は別のオレオレ近似解法で解くことにしています。

最小シュタイナー木問題の例。青が必ず使わなければならない点、灰色が使っても使わなくてもどちらでも良い点。

解法

前述の通り、

経路上の点をいくつか試し掘りすることを繰り返して経路を決める
その後本格的に掘り進める

という流れで解いていきます。

1. 試し掘りパート

試し掘りパートでは、以下を繰り返します。

頑丈さの分布を推定する
最小シュタイナー木問題を解いて仮の経路を決める
経路上の点をいくつかサンプリングする

a. 頑丈さの分布推定

まず頑丈さの推定ですが、これは前提知識の項目に書いたように2次元ガウス過程回帰を用いて推定しました。ガウス過程そのものの説明については上記の本を読んでもらうとして、工夫した点について書いていきます。だいぶ飛ばし気味ですがご容赦ください……。

まずカーネルとして、RBFカーネル $k_1(\boldsymbol{x}_i, {\boldsymbol{x}_j}')=\theta_1 \exp (-|\boldsymbol{x}_i-{\boldsymbol{x}_j}'|^2/\theta_2)$ および観測ノイズ由来のデルタ関数 $k_2(\boldsymbol{x}_i, {\boldsymbol{x}_j}')=\theta_3\delta(i,j)$ を足し合わせたものを考えました。ここで $\theta_1, \theta_2, \theta_3$ はハイパーパラメータで、モデルの対数尤度が最大になるようにグリッドサーチで求めることにしました。*4 *5

このとき、頑丈さ $S_{i,j}$ をそのままモデルに突っ込んで回帰するとイマイチだったので、 $\sqrt{S_{i,j}}$ を突っ込むことにしました。なぜ平方根を取っているかというと、問題の入力生成方法に、

$p=\mathrm{randf}(2.0, 4.0)$ を選ぶ。 $S_{i,j}=\mathrm{pow}(S_{i,j},p)$ と更新する。

という記述があったためです。 $S_{i,j}$ 自体が何かを2〜4乗くらいした関数なので、それをそのまま推定するより2〜4乗する前の何かを推定した方が性能が上がるのでは？というお気持ちから来ています。

これで回帰に使う材料が揃ったので、各点の頑丈さを推定していきます。ただナイーブな2次元ガウス過程回帰の計算量は*6、事前調査済みの点の数を $n$ （私のケースだと $n$ は100くらいのオーダーでした）、推定したい点の数を $m$ として $\Theta(n^3+n^2 m)$ ほどかかるので、 $200\times 200$ 点全てについて推定を行うと重すぎます。そこで、適当に $40\times 40$ のグリッドに間引いて推定し、そこからバイリニア補間*7することで $200\times 200$ 点の頑丈さの推定を行っています。

こうして、各点 $(i, j)$ における頑丈さの2乗の期待値 $\mu_{i,j}$ とその分散 $\sigma_{i,j}^2$ を求めることができたので、これを次のステップで使います。

b. 最小シュタイナー木問題

次に、最小シュタイナー木問題を解いて仮の経路を決めます。

各点 $(i, j)$ における頑丈さの推定値を $\hat S_{i,j}=\sqrt{\mathrm{max}(\mu_{i,j}-\alpha\sigma, 100)}$ として、各点を掘るのに必要な体力が $\hat S_{i,j}+C$ である*8 と考えて最小シュタイナー木問題を解きます。ここで $\alpha$ は適当な定数であり、0.4から0.0までの間で徐々に小さくしていきました。お気持ちとしては、試し掘りパートの初期はコストを楽観的に考えて不確かな点を積極的に掘り、試し掘りパートの終わり際には確実に経路を絞っていく、というような感じです。

最小シュタイナー木問題の解き方ですが、今回は雑な焼きなましを行いました。「使っても使わなくても良い点」のうちどれを使うか決め打てばただの最小全域木問題になるので、クラスカル法を使って簡単に解くことができます*9。そのため、「使っても使わなくても良い点のうちどれを使うか？」を焼きなましで求めました。

このとき、真面目にクラスカル法を解こうとすると毎回ダイクストラで各頂点間の辺のコストを求める必要があり大変です。ここで、「使っても使わなくても良い点」同士は直接辺で結ばないという大胆仮定をおくと*10、クラスカル法に使う各辺の端点のうちどちらかは家か水源となるため、各辺のコストは前計算として $W+K$ 回のダイクストラ（ここで、 $W$ は水源の数、 $K$ は家の数）をすれば求めることができます。すると焼きなましの1イテレーションあたりの計算量は、追加で使う頂点の数を $L$ として $O( (W+K+L)^2 \log(W+K+L) )$ となります。さらに前計算として水源・家のみを考えてクラスカル法を行うと、これらの間の $(W+K)(W+K-1)/2$ 本の辺のうち実際に使う可能性があるのは $W+K-1$ 本であることが分かります。よってクラスカル法で考える必要のある辺の数は $(W+K-1)+(W+K)L$ 本となり、焼きなましの1イテレーションあたりの計算量は $O(L(W+K)(\log(W+K)+\log L) )$ となるため、高速に解くことができます。

焼きなましの近傍としては、

ランダムな点を追加する
ランダムな点を削除する
点をランダムに移動させる

というシンプルな近傍を使いました。これを使って50msも焼けばそれなりに十分な解が得られます。

c. 経路上の点のサンプリング

仮の経路が決まったら、その経路上の点を適当にサンプリングします。このとき、できるだけ不確かさの大きい点を優先してサンプリングするようにしました。また、既に掘った点からマンハッタン距離が一定以下の点は掘ってもあまり情報が得られなさそうなので、そのような点は掘らないようにしています。このあたりはチューニングの余地がありそうですが、詰め切れていないポイントの一つです。*11

ちなみにこのとき、あまりに頑丈すぎる点は途中で掘るのを諦めるようにすると点数が伸びました。そのような点は雑に頑丈さを2500と仮置きしてしまいましたが、モデルへのよりよい情報の与え方もあるようです。

以上a.〜c.を複数回繰り返すことで、どのような経路にするかを確定させました。

本格的に掘り進めるパート

経路が決まったので、掘り進めていきます。このとき、経路上の点と点のちょうど中点を掘ると多くの情報を得られるのではないかと思ったため、そのようにしました。

こちらの進め方は、

各中点の頑丈さの期待値と分散を推定する
中点を掘る

の繰り返しとしました。

a. 頑丈さの推定

先程までは2次元で推定を行っていましたが、だんだん観測済みの点数が増えてくるので計算量が大変なことになってきます。そこでマップ全体ではなく、経路1つ分だけを考えた1次元のガウス過程を考えることで、考慮すべき点の数を減らして計算量を抑えます。

グラフにするとこんな感じです。グラフの左端が水源、右端が家と思ってください。真の頑丈さが青い線で、そのうち緑の点を観測したとき、推定された期待値を黄色の線、そこからのバラつき（今回は $\pm 1\sigma$ 分）を薄い黄色の塗りつぶし領域で表しています。

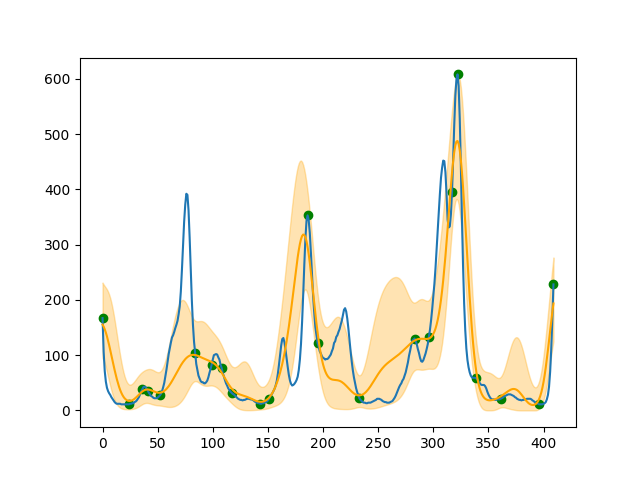
2次元が1次元になっただけなので、ガウス過程回帰のコード自体は使い回しが効きます。

b. 中点を掘る

頑丈さが推定できたので、中点を掘っていきます。このとき、せっかくならパワーをいい感じにして効率良く掘りたいです。もちろん「頑丈さの期待値で掘ってみる」とかでも良いのですが、せっかく分散 $\sigma^2$ も分かっているのでうまく活用したいです。

ガウス過程では、ランダムに出てくる関数 $f(\boldsymbol{x})$ がガウス分布（正規分布）に従うと考えます。よって点 $(i,j)$ において頑丈さが $s$ である確率 $p_{i, j}(s)$ が正規分布の形で出てくるので、消費する体力が最小になるような掘り方はDPで求めることができます。 $dp \lbrack s \rbrack$ を「累計パワー $s$ だけ掘ったときの消費体力の期待値の最小値」とすると、DPの更新式は、

$dp \lbrack s \rbrack = \underset{0 \le t\lt s}{\mathrm{min}} (dp \lbrack t \rbrack + (\int _t^{\infty} {p_{i,j}(\xi)d\xi})\times(s-t+C) )$

となります。*12 何やらややこしい式になってしまいましたが、やっていることは「累計パワーが $t$ から $s$ に増えるときに消費する体力は $s-t+C$ だから、それに確率をかければ消費体力の期待値が出るよね」というだけのことです。なお正規分布の積分は初等関数で表せないらしいので、諦めて台形公式などで数値積分してあげます。*13

DPの計算量評価ですが、とりあえず上記の式をそのまま実装すれば頑丈さの上限を $H$ として $O(H^2)$ となります。ちょっと計算量的に怪しい感じがしますが、実際は $+3\sigma$ くらい上まで見れば99.7%くらいはカバーできるので、実用上十分な解を得ることができます。平均的には $+3\sigma$ は100とか200とかそのくらいの値が多そうなので、2乗になってもそんなに怖くありません。たまに硬い座標に当たったりすると怖いですが、そんなときは適当に状態をまとめてあげる（ $s$ が5の倍数のところだけ考えるなど）と安心です。厳密解は得られませんが、どうせブレるので細かいことを気にしてもしょうがないかなと思います。

そして実はこのDPはうまくstackを使うと $O(H)$ で解くことができるようです。*14

ということで最適な掘り方が求められたのですが、実際にやってみると勢いよく掘りすぎてしまう傾向が見受けられたため、適当な定数 $\beta (1\le\beta)$ を使って、

$dp \lbrack s \rbrack = \underset{0 \le t\lt s}{\mathrm{min}} (dp \lbrack t \rbrack + (\int _t^{\infty} {p_{i,j}(\xi)d\xi})\times(\beta(s-t)+C) )$

とした方が良い結果になりました。あまり時間がなくて原因の分析はしきれていないのですが、おそらく

（特に $C$ が大きいときに）実際の $S_{i,j}$ よりも掘りすぎてしまい、その観測値を使ってガウス過程回帰をするため、推定精度が悪化してしまう
正規分布を仮定すると $s$ が負の領域まで $p_{i, j}(s)$ が伸びてしまい、その辺りをうまく扱えていない

あたりがあるかなと思っています。前者は観測値をガウス過程回帰に与えるときの与え方を工夫すれば改善できたかもしれません。

動画

以上を実装すると、こんな感じの動きになります。

最適解は得られていませんね。まだまだ改善の余地がありそうです。

ガウス過程は2次元と1次元両方やったりしたのですがだいたいそんな感じ。seed=0のスコアは147336点でした。 #AHC018 pic.twitter.com/RmlXVPcDmk
— TERRY (@terry_u16) 2023年2月26日

おまけ: CNN解法

コンテスト序盤はガウス過程の存在すら知らなかったので、ディープラーニングを用いて頑丈さを推定していました。

今回の問題は、2次元画像上の掘った点とその頑丈さからもとの画像を推定するImage to Imageタスクと捉えることができます。以下の図のようなイメージです。

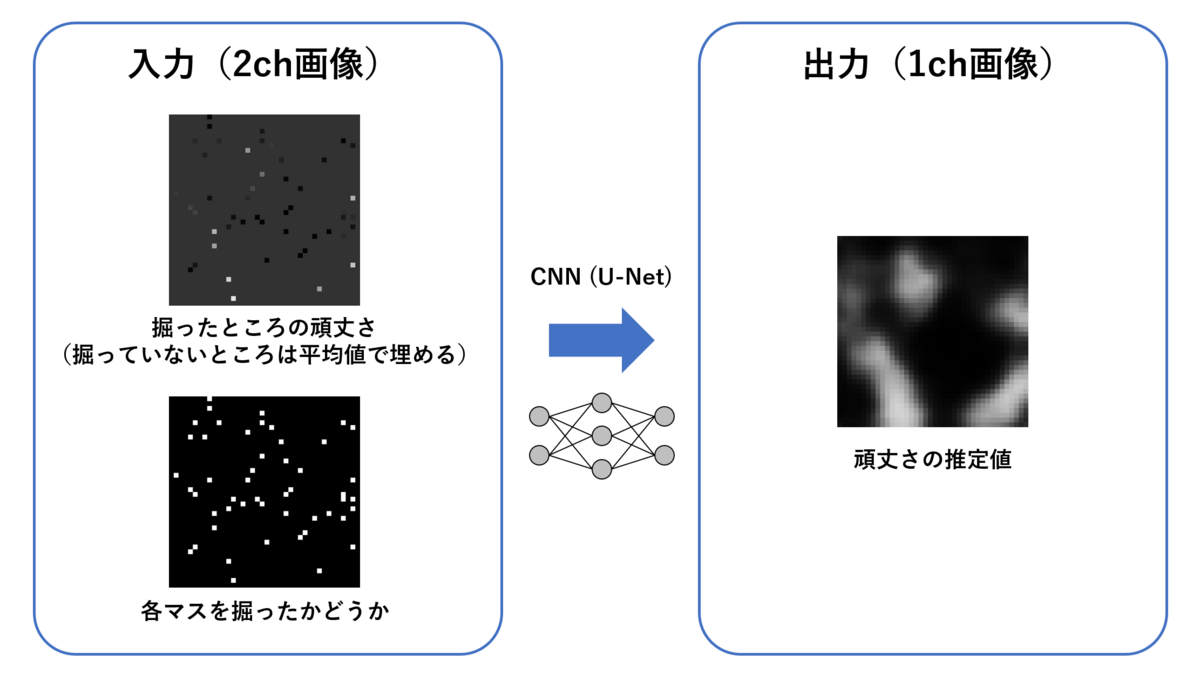
これをCNN（畳み込みニューラルネットワーク）を用いて推定していくことを考えました。今流行りのVision Transformerなどを使っても良いのかもしれませんが、正直理解と実装が間に合う気がしなかったので、比較的古くからあって*15シンプルなU-Netというネットワーク（もどき）を採用しました。エンコーダーで畳み込みとmax-poolingを繰り返して特徴を抽出したあと、エンコーダーの途中の層からコピペ（？）を繰り返しながらデコードすることで画像を生成する手法で、Uの字のような形をしていることからU-Netという名前が付けられているらしいです。

といっても、U-Netは存在を知っていただけで実装したことはなかったので、まあまあ苦労しました。加えてコード長制限に引っかからないようにするとかなり小さなネットワークにせざるを得ず、そこも頭を悩ませたポイントです。

最終的に下図のようなネットワークを採用しました。入力画像は40x40に縮小していて、パラメータ数は34,241個、CNNとしてはかなり小規模なものになっています。*16

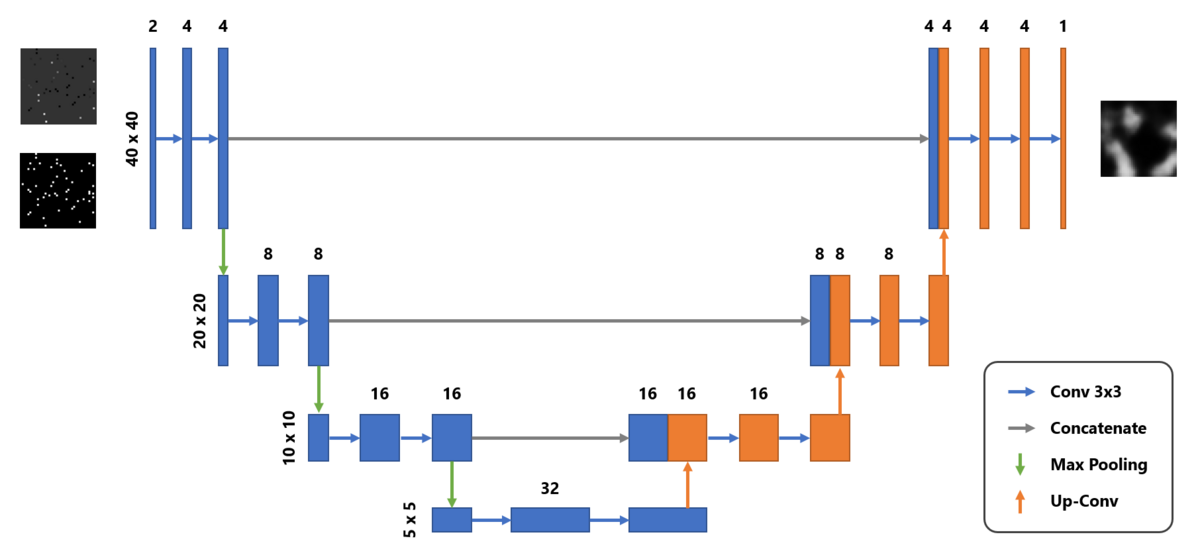
これを学習させたのが下図の右上です。1回の推論に必要な時間は手元PCで4ms程度でした。結構良い感じに推定できている……のですが、分散も求められるガウス過程回帰が上位互換っぽいので残念ながらお蔵入りになってしまいました。CNNのRust移植は結構苦労したのですが、残念……。

日記

参加中の日記は以下に書きました。長いです。

github.com

感想

今回のコンテストでは新しい手法を学ぶ良いきっかけとなり、非常に収穫が大きかったです。自分でもちょっと手法に走ってしまったかなという感覚はコンテスト中にも感じていて、上位を狙うならかっこいい手法に走るより堅実に問題と向き合った方が良いようにも思ったのですが、今回は新しい知識を身に付けることに全力を注ぎました。正直良い順位が取れなくても良いかなと思っていた中で、CNN・ガウス回帰を学んで実装しきった上でそれなりの順位になれたので大満足でした。

一方で体力はかなり削られましたね……。最初の土日はCNNの成立性検証とRust移植に費やされて、木曜（祝日）にガウス過程回帰本を買って勉強して……とやっていたら、まともな提出ができたのが最終日の朝になってしまいました。途中間に合わないかもと思いましたが、腕力でなんとかした形です。さらにガウス過程の勉強では久々に線形代数に触れることになり、しかもそれを1日で詰め込んだので頭が爆発するかと思いました。

問題自体も非常に面白かったです。こういう問題は強い推定手法を持ち込んだ人が優勝という流れになりがち*17かと思いますが、それだけではダメでちゃんとヒューリスティックな手法をうまく設計しないと上位を取れないという塩梅は流石だなと思いながら解いていました。

AtCoderの皆様、そして日本橋ハーフマラソン事務局の皆様、面白い問題をどうもありがとうございました！

*1:コンテストも終わりに近付く木曜日に本を買って、必死に勉強しました。死ぬかと思った……。

*2:ちなみに右上はディープラーニングを用いて予測した頑丈さ分布です。おまけの項目で後述します。

*3:水源同士は繋がなくてもいいから最小全域木問題ではないのでは？と思われるかもしれませんが、水源同士がコスト0の辺で結ばれていると考えれば最小全域木問題に帰着できます。

*4:そもそも尤度という概念すらよく分からなかったので勉強しました……。

*5:問題ごとのパラメータf0, f1などによって最適なハイパーパラメータは大きく変わってくるので、事前に求めるのではなく解きながら求めることにしました。

*6:「ナイーブな」と書いているように、高速化の手段は色々あるようです。今回は余裕がなかったため使いませんでした。

*7:＝2次元の線形補間。

*8:実際はもう少し余計にコストがかかるので、それを加味しても良かったかもしれません。詰め切れていないポイントです。

*9:先に述べたとおり、水源同士はコスト0の辺で結ばれていると考えればよいです。

*10:当然よりよい解を見逃す可能性はありますが、最小シュタイナー木問題パートはさほど本質的でないと考えたので、雑に解くことにしました。正直最小シュタイナー木問題と捉えずダイクストラを繰り返すだけでも対して変わらないのでは？という気もしています。

*11:コードがまともに動くようになったのが最終日の朝だったので、詰め切れていない点が多いです……。

*12:998244353アレルギーなので間違っていないか心配です……。

*13:後から知ったのですが、正規分布の累積密度関数の代わりにロジスティック関数を使うと十分良い近似になるそうです。

*14:アルゴ力さん……。

*15:といっても数年前とかですが。この分野の進展の速さは怖すぎます。

*16:これでも32bit浮動小数点数としてbase64エンコードすると182kB程度になってしまいます。なかなか厳しい……。

*17:それはそれで悪いというわけではないのですが。

TERRYのブログ

最近は競技プログラミングにお熱。

RECRUIT 日本橋ハーフマラソン 2023冬（AtCoder Heuristic Contest 018）解説