トヨタコン決勝お疲れ様でした。
296,099,135,302点で優勝しました!オンサイト初入賞だけでも嬉しいのに、それがまさか優勝するとは思いもしなかったのでとても嬉しいです!
ひさしぶりに解説記事を書いていきます。
問題概要
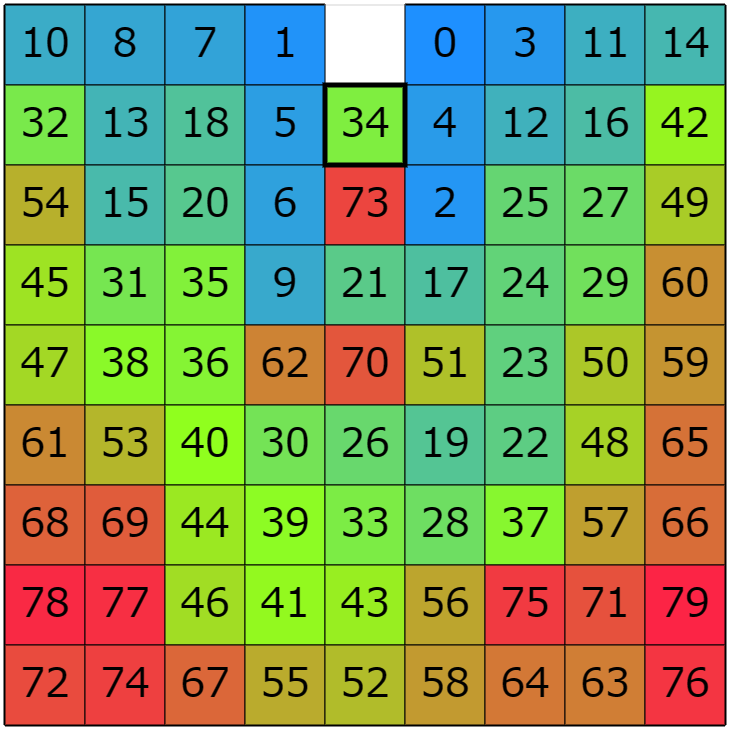
コンテナを倉庫に入れた後、できるだけ順番通りに取り出してね。
ただし倉庫に入れる順番はランダムで、運び込まれてくるタイミングまで何が来るか分からないよ。
前提知識
今回はモンテカルロシミュレーションを使います。あまり聞き慣れない人もいると思うので軽く説明しておきます。
「こちらが選択肢を選んだ後に次の情報として何かが与えられるが、それが何なのかまだ分からない。何が与えられてもいいように、得られるスコアの期待値を最大化するような選択肢を選びたい。」という状況を考えます。このとき、考えられうる全てのケースについて、それが与えられたときのスコアを計算してあげれば当然期待値が求められます。しかし、今回の問題では考えられうるケースの数がコンテナ数を 個として
通りあるので、とても全てのケースについてスコアを計算してあげることはできません。そこで、ケースのうちいくつかをランダムにサンプリングして、サンプリングされたものに対してスコアを計算することで近似的に期待値を求めるのがモンテカルロシミュレーションです。サンプリング数を増やしていけばだんだんと真の期待値に近付いて行くことが期待されます。
なお、AHC的な文脈だと「サンプリングしたケースに対し、適当な方法で最後まで処理を進めて最終的な状態のスコアを計算する」という処理を行うことが多く、これはプレイアウトと呼ばれています。プレイアウトは「完全ランダムな手で最後まで処理する」「貪欲法などで最後まで処理する」などいろんな戦略が考えられます。プレイアウトは高性能な方が実際のスコアを良く模擬しやすい*1のですが、あまり凝った手法を行うと今度は処理が重くサンプリング回数が稼げなくなってしまうので、AHCでは貪欲法が使われることが多いように思います。*2
方針
搬入パートと搬出パートに別れるのですが、まず搬入パートはモンテカルロシミュレーションをしました。毎ターン実行可能な選択肢のうち有望そうなものをピックアップして、それらに対してモンテカルロシミュレーションを行って一番良さそうなものを選ぶという方針です。
搬出パートは「取れるコンテナのうち、一番IDの小さいものを取る」というシンプルな貪欲がベースで、これを焼きなましで軽く改善しました。
どちらかというと搬入パートの方が重要だったように思います。以下、解法を説明していきます。
解法
搬入パート
まずは搬入パートから説明します。モンテカルロシミュレーションを行っていくのですが、まずは強い貪欲を作るのが超大事です。この貪欲の性能で全体の性能が決まります。*3
まず、「どのIDのコンテナを入口からどの距離に置きたいか」というリストを作っておきます。直感的にはIDの小さいコンテナは取り出しやすいように入口近くに、IDの大きいコンテナは入口から遠くに置きたいです。なのでそれを満たすように距離を決めていきます。
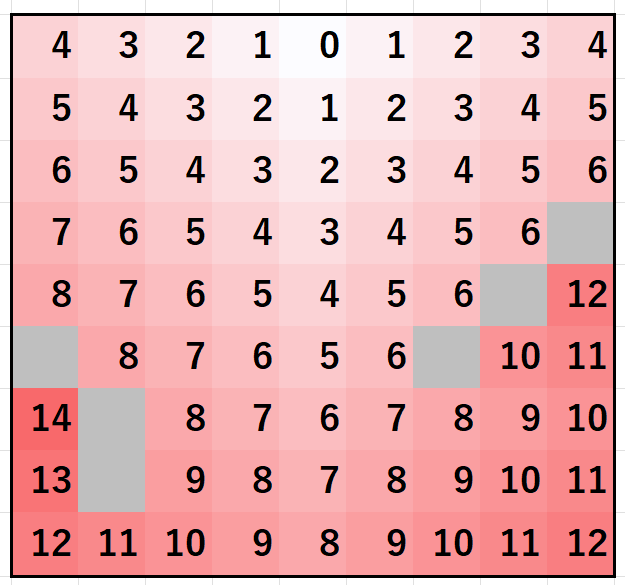
入口からBFSをして、下図のように各マスの入口からの距離を求めておき、IDの小さい順に距離の小さいものをアサインしていきます。例えば下図の例では、ID0~2は距離1、ID3~7は距離2のところに置きたいというように決めておきます。このIDごとに置きたい距離を とします。この
や入口からの距離は常に固定とし、マスがコンテナで埋まっても再計算はしないものとします。*4
そのうえで、合法手となるマスを置き場所の候補として、以下のような貪欲をします。
- 今のIDのコンテナを置きたい距離を
、そのマスの入口からの距離を
とする
として、
ならペナルティは
、
ならペナルティは
とする
- これは近くに置きすぎると後が大変なので、できるだけ遠くに置きたいという気持ちを込めている
- タイブレークとして、できるだけ外周からのマンハッタン距離が近いマスを選ぶようにする
- これは中央ではなくできるだけ端に寄せたいという気持ちを込めている
この貪欲だけで289,595,414,754点が出たので、あとはこれを使ってモンテカルロシミュレーションをします。コンテナが来るたびに、以下のシミュレーションを回します。
- 上記の貪欲の評価値が高い7箇所を対象とし、それぞれについてコンテナ順のパターンを35ケース与えて残りの搬入・搬出を実施し、そのときのスコアの期待値を求める
- 搬入パートのプレイアウトは上記の貪欲をそのまま使う
- 搬出パートのプレイアウトはアクセスできる荷物のうち最もIDの小さいものを取り出す貪欲を行う
これでそれらしい搬入ができるようになりました。
なお、貪欲を行うときに「置いて良い場所」を列挙する必要があるのですが、これは「グラフとして見たときに関節点*5でないマス」であるので、lowlinkを使うと で高速に列挙が可能です。*6モンテカルロシミュレーションを行うためには速度が欲しいので、かなり有効なように思います。
搬出パート
搬出パートは「取れるコンテナのうち、一番IDの小さいものを取る」というシンプルな貪欲がベースで、これを焼きなましで軽く改善しました。
焼きなましを考える前に、貪欲の捉え方を変えてみます。「取れるコンテナのうち、一番IDの小さいものを取る」という貪欲でしたが、これを「取れるコンテナのうち、一番優先度の高いものを取る」としてあげます。「IDが小さい方が優先度が高い」と考えれば、両者の処理は同じになります。
そしてその優先度を焼きなまします。近傍はあまり工夫していなくて、適当に「あるIDの優先度を適当な順番に挿入する」としているだけです。焼きなましと言いつつ、結局温度はだいぶ低くなったので山登りで十分かもしれません。スコアは「その優先度で貪欲をしたときの生スコア」としています。
多分ガチれば焼きなましよりビームサーチの方が強いんじゃないかという気がしていますが、焼きなましは「評価関数を考えるのをサボってもそこそこ良い解になる」「時間調整が容易なため、モンテカルロシミュレーションでブレた実行時間を吸収しやすい」という点が嬉しいです。
ちなみに取れるコンテナの列挙を行う際、毎回BFS/DFSを行わずとも取り除いたコンテナの4近傍を優先度付きキューに突っ込んでいけば高速に差分更新が可能……なのですが、今回はサボりました。時間的な余裕がなかったため……。
これらの搬入・搬出を合わせると以下のような挙動になります。それらしい動きになっているんじゃないかと思います。
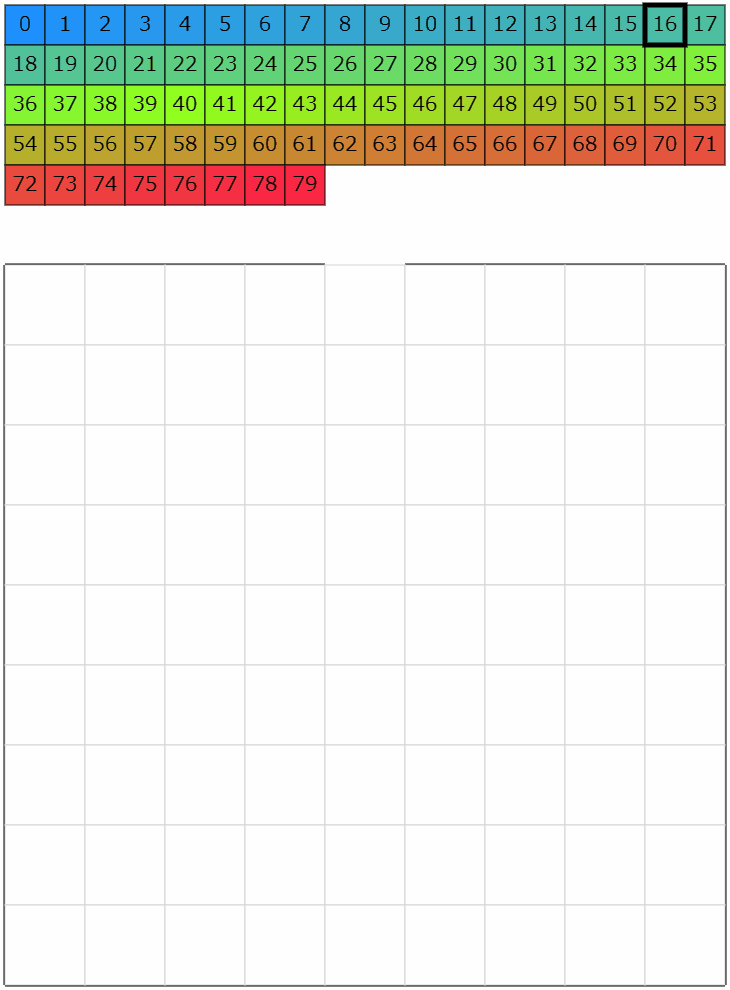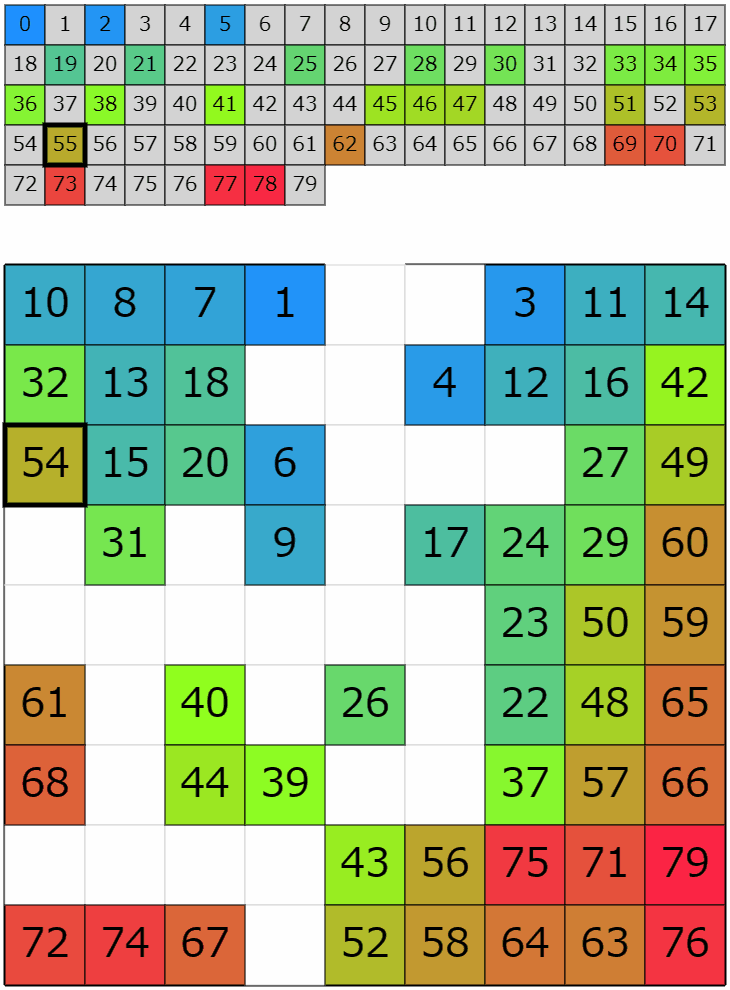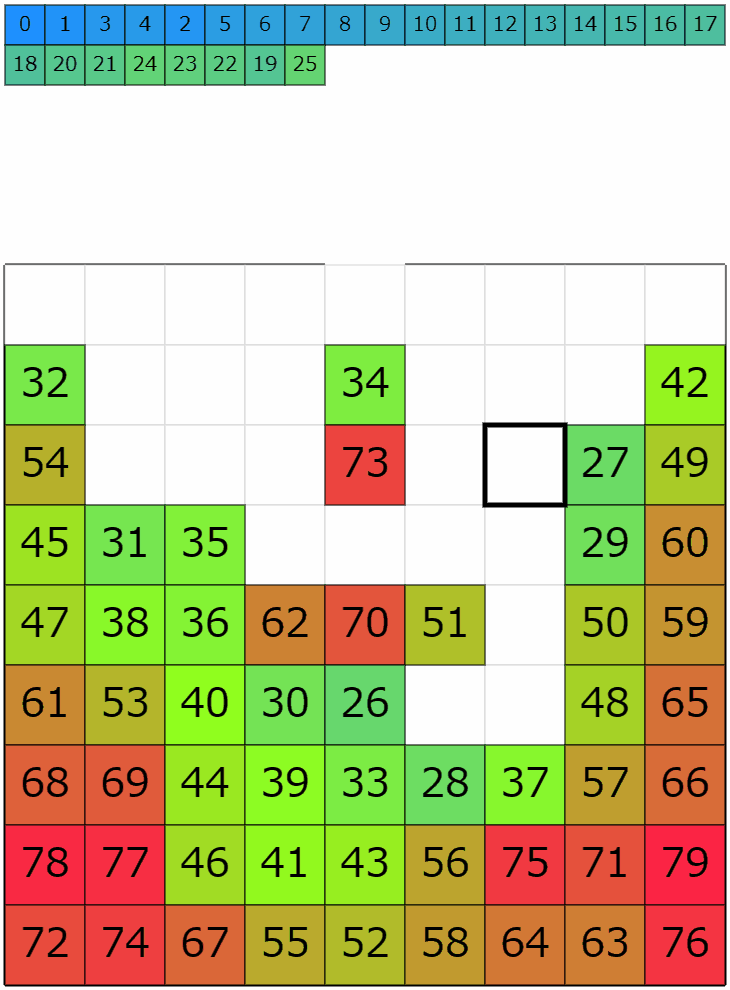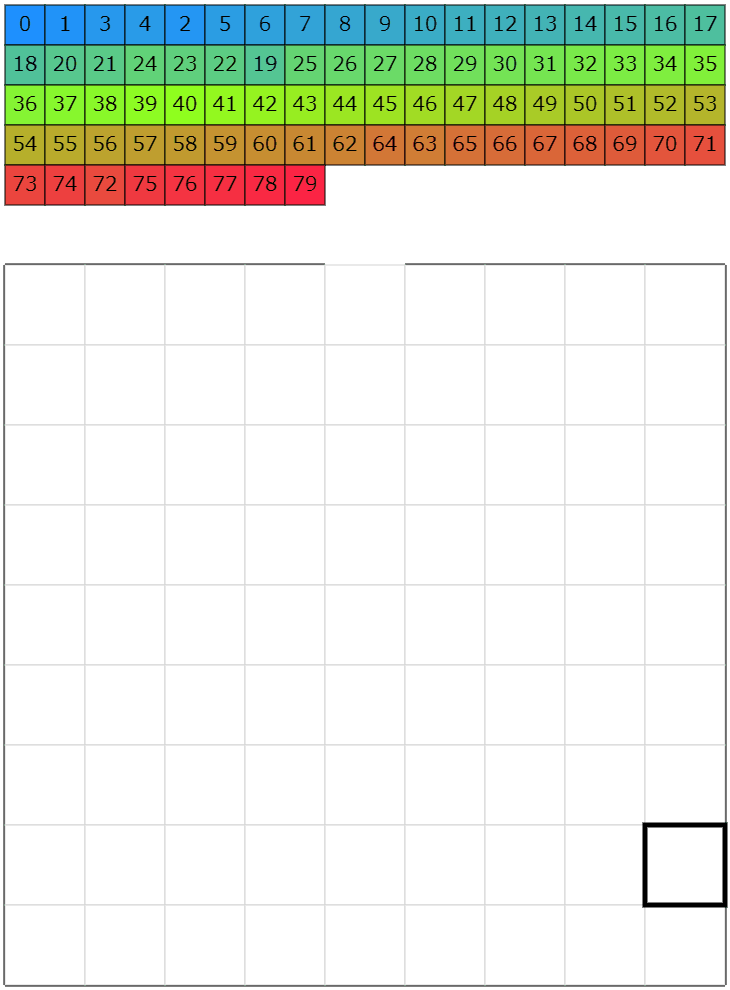
コンテスト中の動き
コンテスト中、いつ何をしていたかを思い出せる範囲で書き出していきます。こんな動きをしているんだという参考になれば幸いです。
常体の方が書きやすいので、常体で書きます。
validな解を出す(~1h13m)
問題を読む。面白そうだが何をすれば良いのかさっぱり分からん。モンテカルロか?しかし良い貪欲がさっぱり思い付かない。ランダムプレイアウトして良い結果になるとも思えないしなあ……。
考えていてもしょうがないので、まずはvalidな解を提出することにする。置ける場所はlowlinkで列挙できるので、とりあえず適当な合法手を何も考えずに選ぶコードを書く。搬出もよくわからんのでとりあえず取れるコンテナのうちIDの小さい順に取っていく雑貪欲にする。トヨタ実課題コンでも似たようなものを見た気がするが、多分最適手順ではないので後で改善の余地あり。
lowlinkの実装に地味に時間を取られた上、搬出パートのなんでもないBFSで謎に死ぬほどバグって時間を溶かしてしまった。1時間ちょっと経ったところで提出。237,603,250,321点で真ん中より下の方だった記憶。
距離順で貪欲をする(~1h26m)
3時間半コンテストでモンテカルロまで実装しきれる気が全くしないので、貪欲を頑張ることにする。後になって思うとこれはかなりプラスに働いて、これによって強い貪欲を作ることに集中できたように思う。これは自分あるあるなのだが、手法ベースの戦略だとついついその手法に頼りがちになってしまうので……。
直感的には、IDの小さいコンテナは近くに、大きいコンテナは遠くに置きたい。なので入口からBFSをして、できるだけそれを満たすような場所に置いていくことにする。ちゃっちゃと実装して提出すると283,993,349,088点で、10位前後くらいだったはず。凝ったことをしていないのでそんなに良くないかなと思っていたが、思いのほか良い順位でテンションが上がる。
貪欲を強くする(~1h51m)
自分の実装力を信用していないので、貪欲を強くする方向でいろいろ試した。
ビジュアライザを見ると、最後にやたら長い一本道が爆誕しており、そこに置く以外の選択肢がない状況になってしまっている。距離とIDごとのアサインを初期状態のもので固定してしまっているが、コンテナを置くたびに毎回計算し直した方が良い気がするのでやってみた。280,464,713,420点。うーん下がったな。ボツ。
次に考えたのが、できるだけ近くではなく遠くに置いていきたいという点。今の評価関数だと置きたい距離より近くても遠くても同じペナルティだが、近場が埋まっていくと選択肢が減っていって良くなさそうなので、置きたい距離より近くに置いた場合はペナルティを重くした。これを投げると288,023,808,928点で、3位くらい?になった記憶。ここまで効くとは思わなかった。いいね。
またビジュアライザを見ると、序盤から積極的に中央付近に置いているのが気になった。中央付近に置くと後々邪魔になるので、できるだけ端に置いていって欲しい。ということでタイブレークとして外周からの距離を評価に入れたところ、289,595,414,754点になった。どうしちゃったんだ?こんなに貪欲の評価関数ガチャを当てるなんてぼくらしくないぞ?
搬出パートを焼きなます(~2h35m)
ここからは搬入パートでモンテカルロするか搬出パートで焼きなましするかの二択なのだが、未だに自分の実装力を信じていないので実装しやすそうな後者を選択した。どう考えても前者を優先すべきです。ありがとうございました。
焼きなまし方は5分くらいで思い付いたので実装する。焼きなまし自体の実装は10分くらいで終わって、それ以外のリファクタリングに時間がかかった印象。実行してみると結構改善されている印象がある。よしよし。提出すると291,298,724,057点。あとは貪欲の「近い方がペナルティ重い」係数を微調整して291,853,974,269点。これは優勝争いに絡めるかも。
余談だが、ジャッジアップデートの影響でRustの乱数ライブラリの書き方が変わっており、コンパイルエラーで時間を浪費してしまった。環境構築はしっかりしておこう!
モンテカルロシミュレーションをする(~3h00m)
さすがにモンテカルロシミュレーションをやった方が良さそうだったので、モンテカルロシミュレーションを実装する。適宜リファクタリングして各種処理を部品化していたので、思ったより実装コストはかからなかった。投げるより手元PCで回した方が早そうだったので手元実行。シミュレーション回数が少ないと全然ダメだったが、回数を増やすと目に見えて点数が伸びて面白かった。
実装終わったのが2h58mくらいで、もうすぐ順位表凍結というタイミングだった。そのときの順位表1位が294.5G点だったのだが、手元100ケースで回した感じだと295G点には乗りそうな勢い。ちょっと潜伏気味で行った方が良いと判断して、順位表が凍結されたタイミングで提出。295,014,380,515点。
微改善(~3h30m)
残り30分は微改善に費やした。この判断は微妙で、シミュレーション回数を増やすと点数が伸びることが分かっているんだから搬出パートの差分計算を実装した方が良い。が、そこまで頭が回らなかった。
モンテカルロシミュレーション回数を増やしたり、シミュレーションをする候補手の数を増やしたり、焼きなまし時間を残り時間いっぱいまで可変にしたりした。こう書いてみると大したことやってないな。とはいえそれなりに伸びて、296,099,135,302点でフィニッシュ。自分にしては上出来だったように思う。
感想
9ヶ月ほどまともなレート変動がない状況が続いていた*7のでたまには良い成績を取りたいと思っていたのですが、まさかオンサイト決勝という大舞台で優勝することができるとは思っていなかったので本当に嬉しいです。
直近のAHC022はコロナ感染で途中離脱し、ヒューリスティックランキング11位に落ちて金冠剥奪となりテンションが下がっていたのですが、今回優勝して一気にランキング4位、レート3000超えで無事金冠奪還することができました。まさかこんなに早く金冠を取り返せるとは思っていなかったです。1年分のレート変動を一気にもらえたような気がします。
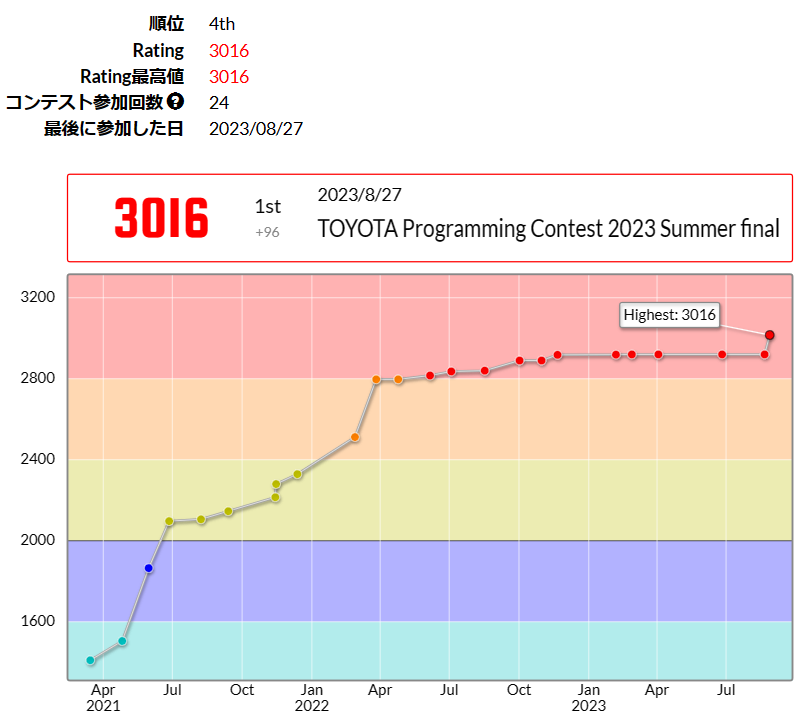
コロナ発症から9日目ということで、会食となると他の人にうつしてしまうリスクがあるかなと思い、懇親会を辞退せざるを得なかったのが心残りではあります。次回のオンサイトでは万全の体調で懇親会まで楽しみたいですね。
最後に、今回のトヨタコンの関係者の皆様、一緒に戦った参加者の皆様、オンサイトコンテストをratedにしてくれた方、本当にありがとうございました!今後もっともっとヒューリスティックコンテスト界隈が盛り上がってくれることを期待しつつ、私もそのお力添えができると良いなと思っています。
追記(延長戦解法)
TOYOTA AHC 至高のアルゴリズム解説会で発表した299,238,709,281点解法のスライドはこちらです。
*1:というか「ある本命の手法でプレーしたときの期待値」を求めたいので、その本命の手法と同じにしたいです。
*2:まあ今までAHCでモンテカルロシミュレーションが出るケースはそんなに多くなかったので、サンプル数は少ないのですが……。
*3:まあそうやっていつも強い貪欲が作れるなら苦労しないのですが。AHC015とか……。
*4:再計算した方が良さそうな気もしたのですが、スコアが下がったのでやめました。
*5:その頂点を取り除いたときに、グラフが非連結になるような頂点のことを関節点と言います。
*6:lowlinkはABCなどではあまり出てくる機会がないように思います。コンテスト本番でlowlinkを有効に使えたのは初めてな気がするので、ちょっと嬉しいです。
*7:去年HTTF予選以降、9ヶ月かけてレートが+2しか伸びていませんでした……。