HTTF2024お疲れ様でした。1,949,540,679,822点で6位（perf. 2836）です。長期コンで良い成績を取るのは1年ぶりだったので嬉しいです。今回も解説記事を書いていきます。

問題概要

お掃除高橋くん2号をいい感じに動かして部屋を綺麗に保ってね。

atcoder.jp

メタ戦略

適当な貪欲で問題の雰囲気を掴んだあと、どのような戦略で取り組むべきか考えました。

色々考えていくと、

完全情報ゲーなので焼きなましかビームサーチが基本線になりそう
無から焼きなましで解を生成するのは明らかに無理筋
しかしTSPチックな面もあるので、最上位を狙うにはどこかで焼きなましを入れないとキツそう（ビームサーチでTSPを解くのはむずい）
ということで「何らかの方法で初期解を作って、それを焼きなます」という方針にしたい
初期解を「一番汚れているマスに行く」などとすると、大局的にはいい解にならなさそう
良さそうな評価関数も思い付かないので、まずは「最終的にどんな解になると嬉しいか」を考える

というような思考の流れになりました。この戦略が今回は上手くハマってくれたのかなと思います。*1

解法

ざっくり以下の流れで解きました。

(どういう解になってくれると嬉しいかイメージしておく)
「頂点列 $P$ に貪欲に頂点を挿入 → 焼きなまし → 頂点列 $P$ のループを2倍に」を繰り返して初期解 $P$ を作る*2
初期解 $P$ の頂点間をダイクストラで繋いで経路 $R$ を作り、これを焼きなます

AHC027お疲れ様でした！48,809Gで暫定6位。
数式をガチャガチャしたり焼きなましで実験したりすると、2マスの汚れやすさがd_1:d_2のときはざっくり√d_1:√d_2くらいの頻度で訪れると良さそう（これが下界になる？）なのでその状態を目指します。(1/5) #AHC027 pic.twitter.com/xHiGfsvnQD
— TERRY (@terry_u16) 2023年12月10日

最終的な解のイメージ

まず最終的にどんな解になってほしいかのイメージを作っておきます。簡単のため、以下のように問題を緩和します。

ロボットの位置を考えず、各マスを任意のタイミングで掃除できるとする
掃除タイミングは整数値である必要はなく、任意の実数時間を取れるものとする

このとき、長さ $L$ の操作列の中でマス $(i, j)$ を掃除する回数を $c_{i,j}$ とすると、 $L=\sum_{i=0}^{N-1}\sum_{j=0}^{N-1} c_{i,j}$ となります。このときのマス $(i,j)$ の汚れの総和 $S_{i,j}$ は底辺 $\frac L {c_{i,j}}$ 高さ $\frac {d_{i,j}L}{c_{i,j}}$ の三角形が $c_{i,j}$ 個あることから $S_{i,j}=\frac 1 2 \times \frac L {c_{i,j}} \times \frac {d_{i,j}L}{c_{i,j}} \times c_{i,j} = \frac{d_{i,j}L^2}{2c_{i,j}}$ となります。したがって平均汚れ $\bar S$ は $\bar S =\frac{L}{2}\sum_{i=0}^{N-1}\sum_{j=0}^{N-1}\frac{d_{i,j}}{c_{i,j}}$ となり、これを最小化するような $c_{i,j}$ を求めればよいです。これを解くのは難しいのですが*3、マスが2つのときを考えたり焼きなましで実験したりすると、マス $(i,j)$ は汚れやすさの平方根 $\sqrt{d_{i,j}}$ に比例する頻度で掃除すると良いことが分かります。ということで、できるだけそれに近い解を求めていくことにします。

ちなみにこれはスコアの下界になる（はず）なので、得られたスコアを下界で割って正規化しておくと手元実行での管理が楽になりました。最終的な解ではだいたい下界の1.1～1.2倍くらいのスコアになりました。

初期解の構築

前節の議論により、各マスの汚れやすさの平方根に応じた頻度で掃除すれば良いことが分かりました。しかしピッタリ $\sqrt{d_{i,j}}$ に比例した頻度で掃除することは困難なので、2冪で丸めてしまうことにします。このようにすることでルートが作りやすくなります。例えばマスA, Bが汚れやすくマスC, Dが汚れにくい場合、 A→B→C→A→B→D→A→…… のようなルートを作ることでA, Bを2回掃除する間にC, Dを1回掃除するという動きを達成できます。

このようなルートを構築するため、以下のような処理を行いました。

空の頂点列 $P$ を用意する
$256\le d_{i,j}$ であるようなマスについて、 $P$ に入っている頂点集合から遠い順（ $P$ が空の場合は適当な順）に $P$ へ挿入していく。挿入箇所は貪欲に決める（後述）
頂点列 $P$ を焼きなます
頂点列 $P$ を2つ連結したものを新しい $P$ とする
$64\le d_{i,j}\lt 256$ のマス、 $8\le d_{i,j}\lt 64$ のマス…… についてそれぞれ2.をしたあと3., 4.を適用する処理を繰り返し、全てのマスが $P$ に含まれるまで処理を続ける

4.の処理を入れるところがキモで、これによって似たようなループが2冪個作られていきます。以下のようなイメージです。

[1回目]
A → B →

[2回目]
A → B → C → A → B → D → 

[3回目]
A → E → B → C → A → F → B → D → A → G → B → C → A → H → B → D →

貪欲パートでは、各マスを挿入した後の生スコア（ここでは $P$ に1回以上追加したことのある頂点のみを考えて、頂点間は最短経路を通ったものとしてスコアを計算する）を評価関数として貪欲に決めました。このとき全部の挿入箇所について愚直にスコア計算をすると間に合わないので、 $P$ の経路長の増加量が小さい頂点を複数個ピックアップしてから、それらについて全探索しました。*4

焼きなましパートの評価関数もほぼ生スコアなのですが、「 $P$ に含まれる各マスからBFSして各マスをグループ分けし、マス $(i,j)$ が含まれるグループの大きさを $s_{i,j}$ として、マス $(i,j)$ からマス $(i',j')$ への移動は $\mathrm{dist}( (i, j), (i', j') ) + 0.5s_{i',j'}$ かかる」とした上で、貪欲パートと同様のスコア計算を行いました。近傍は「1マス削除して、適当なところに挿入する」「連続する複数のマス削除して、適当なところに挿入する」「2-opt」の3つとしています。

経路の改善

初期解を焼きなましで改善していきます。

頂点列 $P$ は $P_k$ と $P_{k+1}$ が隣接しているとは限らないため、まず $P_k$ と $P_{k+1}$ の間でそれぞれダイクストラ*5をして経路を繋ぎ、これを経路 $R$ とします。

これに対して焼きなましを行います。スコアは生スコアを愚直に計算、近傍は「 $P$ の適当な箇所にマスを挿入して $R$ を乱択ダイクストラで繋ぎ直し」「 $P$ の適当なマスを削除して $R$ を乱択ダイクストラで繋ぎ直し」を採用しました。

以上を実装すると、以下のような解が得られました。汚れやすいところを定期的に回りつつ、いい感じに全マスを掃除することができています。

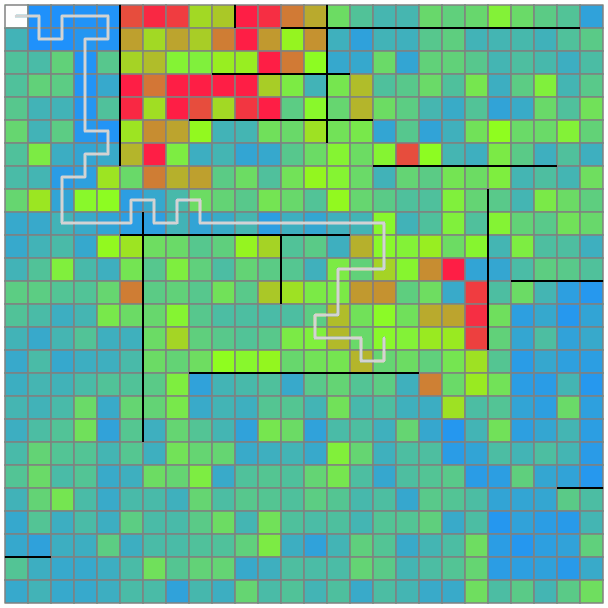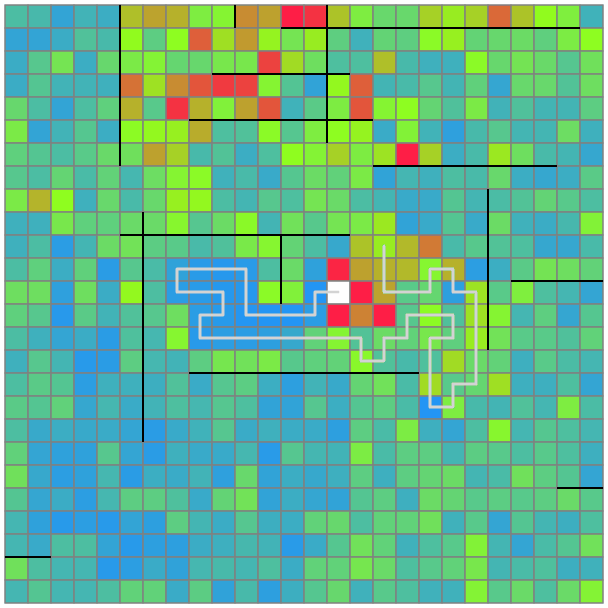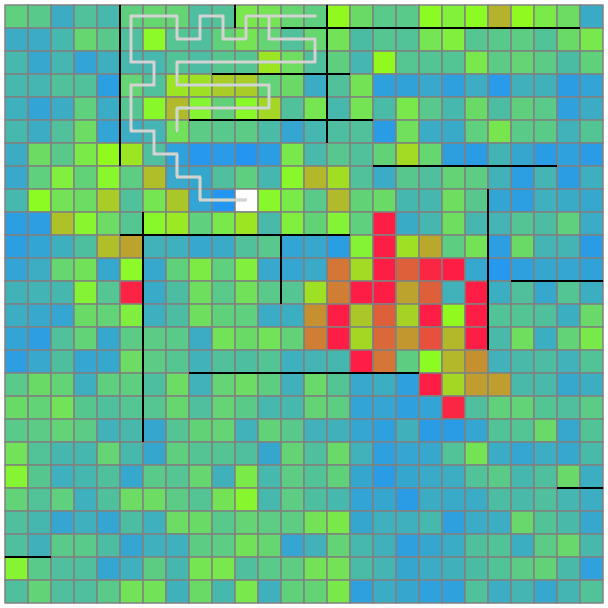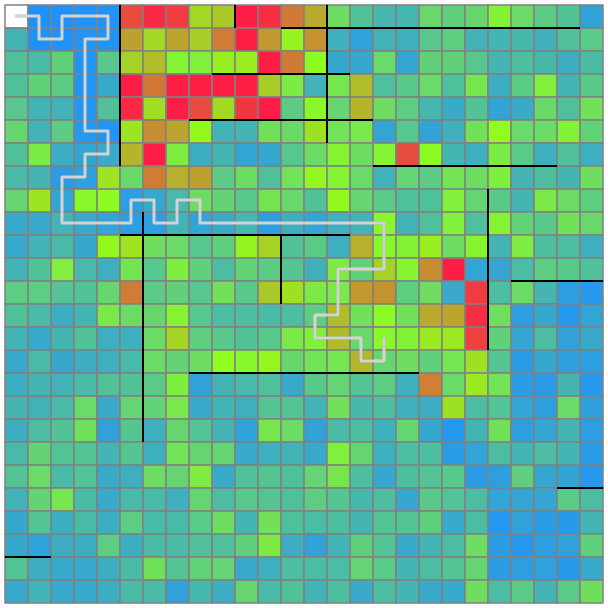
感想

最初はどのように手を付ければ良いか全く分かりませんでしたが、上手く問題の性質を捉えることで考察が進むとても面白い問題でした。焼きなましの差分計算を思い付ければもっと伸びたかもしれませんが、この辺は経験値不足だなあと。「任意箇所の更新は無理でも、どこか1箇所に限定すれば高速に差分計算できるかも」など、いろんな切り口で考察するべきですね。

HTTFは私がヒューリスティックコンテストにハマるきっかけのコンテストだったので、去年に引き続き良い成績が残せてとても嬉しいです。今回も開催して頂きありがとうございました！

*1:別に他の回で考えていないわけではないのですが、噛み合わないときはなかなか噛み合わない……。

*2:ここで、「頂点」は「マス」と同義で使っています。

*3:ちゃんとやると解析的に解けるらしいです。

*4:ちなみに $P$ に追加する頂点集合について、理論的には $d_{i,j}$ が2冪となる場所（256, 64, 16, 4, 1）で区切るのが良いのですが、実際は少しずらした方が良さそうだったので $N$ ごとに実験的に決めています。