AHC011お疲れ様でした。2,535,278,443点の13位で、ついに赤コーダーになることができました！

terry_u16さんのAtCoder Heuristic Contest 011での成績：13位
パフォーマンス：2655相当
レーティング：2797→2816 (+19) :)
Highestを更新し、五段になりました！#AtCoder #AtCoderHeuristicContest011 https://t.co/JTyipIXQwY

ついにヒューリスティック赤コーダーになりました……！ pic.twitter.com/0bSSSuEutX
— TERRY (@terry_u16) 2022年6月7日

いつものように解説記事を書きます。当然ヒューリスティックコンテストに模範解答はないので、あくまで解法の一例として。

問題概要
方針
解説（完成図作成パート）
解説（スライドパズルパート）
- 完成図の改変
- タイル合わせ
細かいテク
- IDA*の仕切り直し
- Zobrist Hash
日記
感想

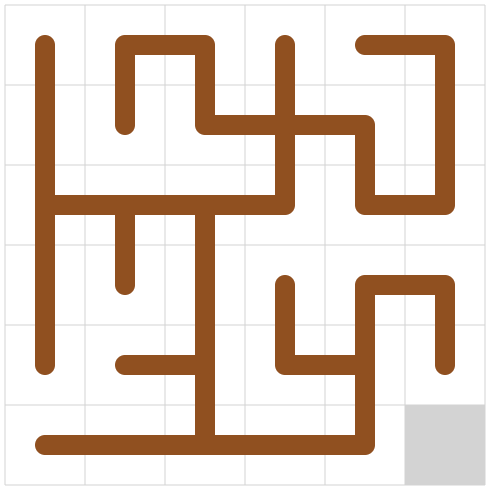
問題概要

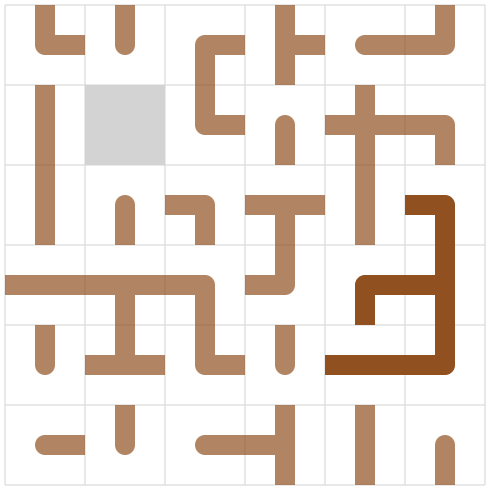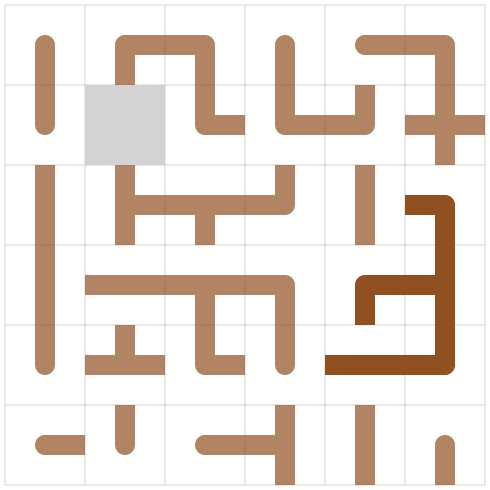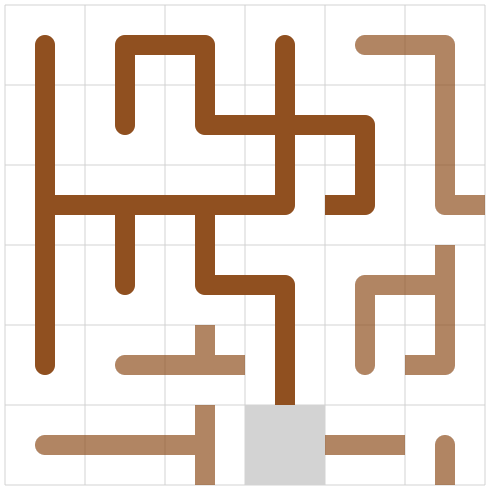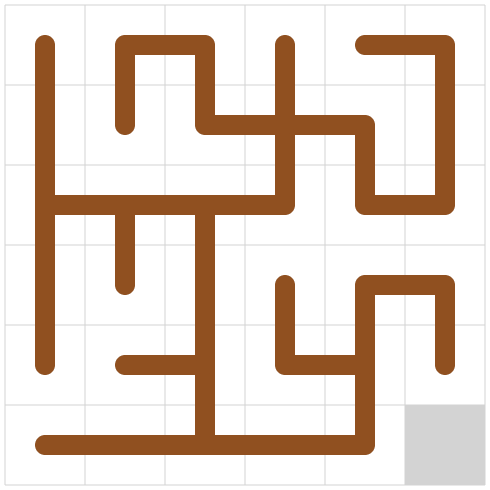
スライドパズルを完成させてね。完成図はなくしちゃったからそれっぽく捏造していいよ。

atcoder.jp

方針

木の作成もスライドパズルもそれ単体の時点で既にめちゃくちゃ難しくて両方同時に解ける気がしないので、まず完成図を作ってからそれに合わせてスライドパズルを解く方針としました。

完成図の作成には焼きなましを、スライドパズルの解法には双方向IDA* *1 を使いました。双方向IDA*という名前を聞き慣れない方も多いかと思いますが、双方向IDA*はIDA*をスタートとゴールの双方向から行ったもので、IDA*はA*とほぼ同じアルゴリズムで、A*とは「こっちに行った方が早く着きそう」みたいな情報を考慮したダイクストラです。要するに初期盤面と完成図の両方からダイクストラです。むずすぎ。後ほど説明します。

スライドパズルパートでは基本的に1行・1列ずつ合わせていきます。このとき欲しいパネルが遠くにあると手数がかかって嬉しくないので、欲しいパネルが近くになるように焼きなましで都度完成図をいじりながら進めていきました。

解法の流れは以下の通りです。

完成図作成パート
1. タイルの枚数を無視して、適当な全域木からなる盤面を作る
2. 木構造を保ったまま、焼きなましによりタイルの枚数を合わせる
スライドパズルパート
1. 次の行・列が合わせやすいように焼きなましで完成図をいじる
2. IDA*を使って1行・1列分を合わせる
3. a.～b.を繰り返す
4. 残り5x5以下になったら行・列を一度に合わせていく
5. 残り3x3になったら全部まとめてIDA*で合わせる

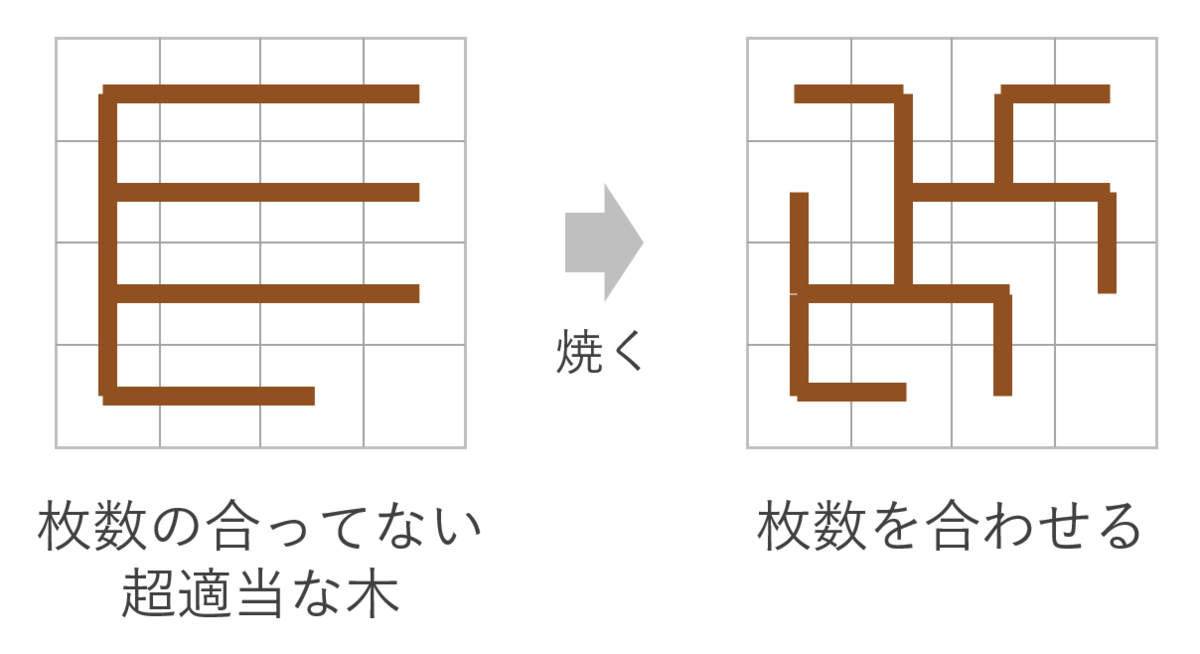
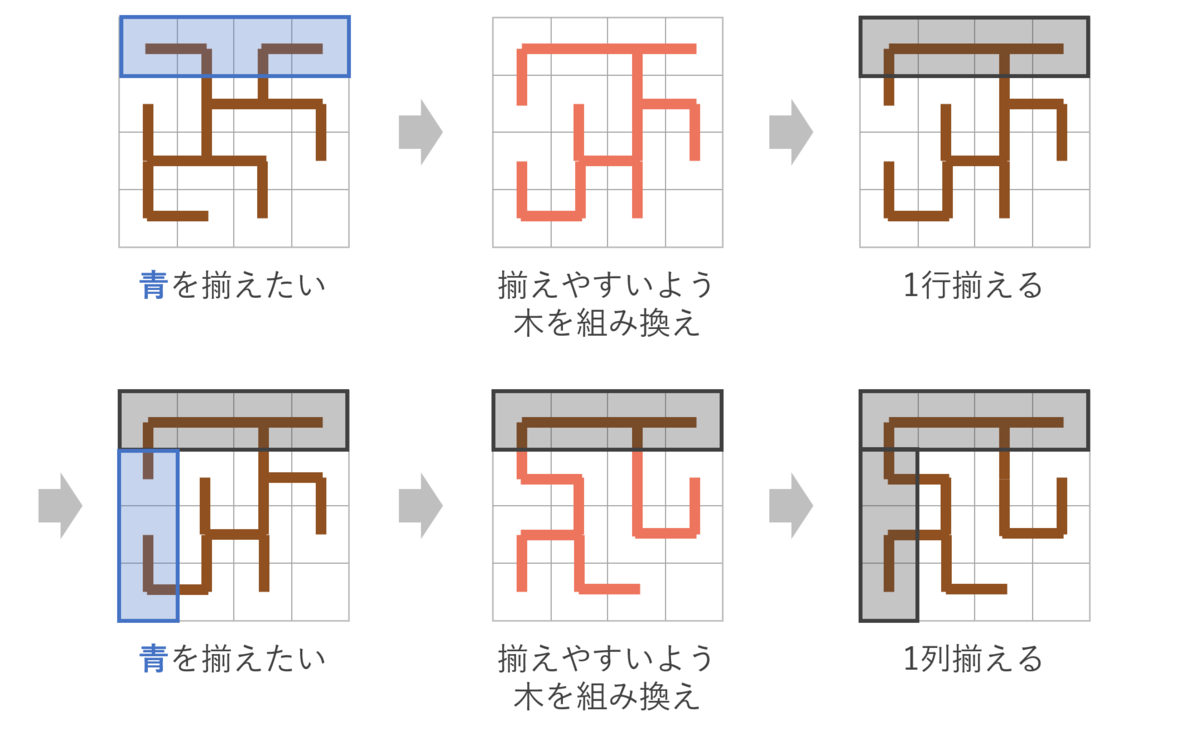
※図ではタイルの枚数が揃っていませんが、実際は枚数がピッタリ合う状態を保ったまま完成図をいじっていきます。

解説（完成図作成パート）

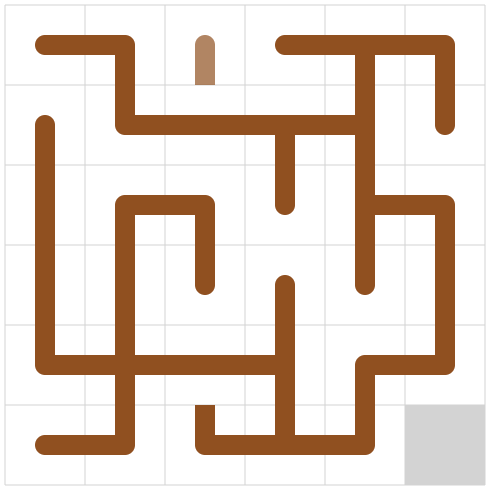
焼きなましにより完成図を作っていきます。前述した通り、まずはタイルの必要枚数を無視してしまい、適当な全域木で初期解を作ります。本当に適当でよいです。

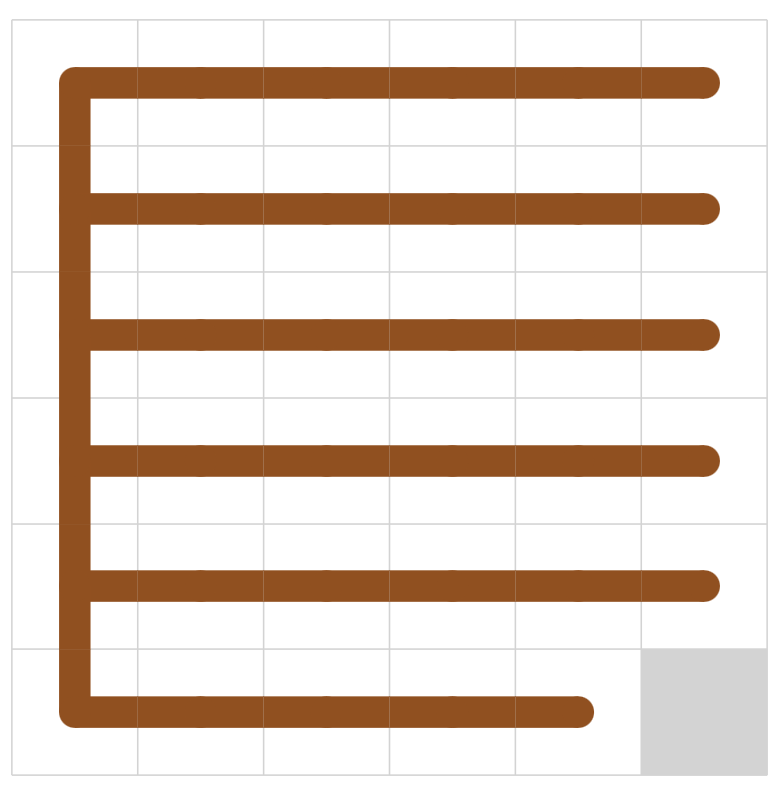
全域木が作れて嬉しいですが、タイルの枚数が違うので当然完成図にはできません。そこで、木構造を保ったまま変形させていき、タイルの枚数をピッタリ合わせることを目指していきます。木構造がこわれる*2と嫌なので、「木の1つの辺を切断して、代わりに別の辺で繋ぎ直す」という操作を近傍として焼きなましました。繋ぎ直すときにどこに辺を足せば連結になるかどうかの判定は $\Theta(N^2)$ の愚直DFSで行っていますが、特に速度面がネックになることはありませんでした。*3

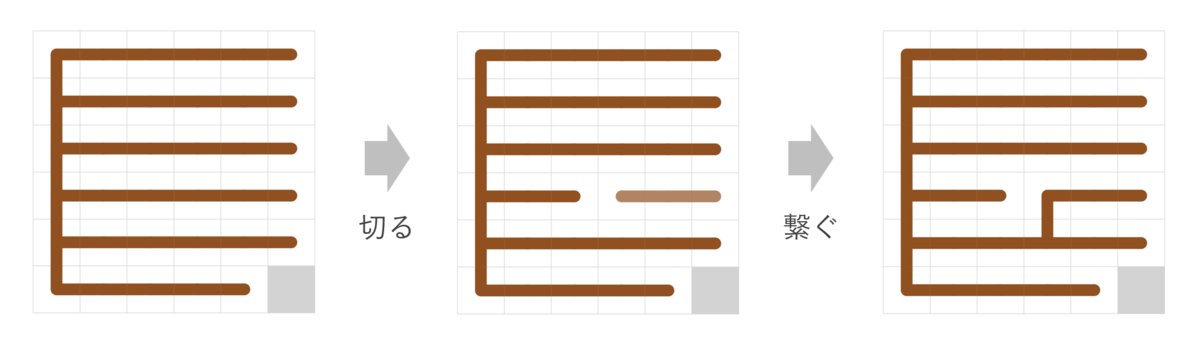
ランダムに操作するだけだと運が良くない限り枚数が一致しないので、タイル $i$ $(0\le i\le15)$ の使用枚数を $a_i$ 、目標枚数を $b_i$ として、評価関数を $\sum_i (a_i-b_i)^2$ と設定し、これを焼きなましで最小化しました。このようにしてあげると0.1秒もかからずにいっぱい木が見つかるようになるので、とりあえず最初に見つかったものを完成図としてあげることにしました。

余談ですが、当初はこのパートを「タイル数を合わせたまま、初期盤面から2点swapで木を完成させることを目指す焼きなまし」を使って解いていました。評価関数は連結成分 $i$ の大きさを $m_i$ 、ループ数を $l_i$ として、 $\sum_i 0.8^{l_i} m_i^2$ としていました。*4 これだと0.5秒回して成功率は7～8割くらいで、失敗した場合は何度も焼きなましを行って誤魔化す必要がありました。焼き方を変えることによってかなり性能が上がった印象です。*5

解説（スライドパズルパート）

完成図ができたので、それを目指して双方向IDA*を使ってタイルを合わせて行きます。全部一気に合わせるのは現代のコンピュータだと不可能 *6 なので、以下のように少しずつ合わせていくことにしました。

6x6以上の領域が残っている場合は、1行・1列ずつ合わせる
5x5以下になったら、行・列をまとめた「く」の字型の領域を合わせる
3x3になったら、全部一気に合わせる

なお、ある行・列を揃える前に、「その行・列のタイルを持って来やすいように焼きなましで完成図を改変する」という処理を挟んでいきます。完成図の改変→実際に揃える→次の行・列へ……の繰り返しです。*7

完成図の改変

使うタイルの種類さえ合わせれば完成図を自由に改変できるので、焼きなましを使って次の行・列を合わせやすいように完成図を捏造していきます。

どういう完成図が「合わせやすい」のかという評価はかなり難しいのですが、ここでは「現在のタイルの位置と完成図のタイルの位置のマンハッタン距離の二乗和（と前述の $\sum_i (a_i-b_i)^2$ との線形結合）」を評価関数として焼いています。なおこのとき、次の行・列以外のタイルは全て無視しています。焼きなましの近傍は先ほどのものと全く同じで、タイル数が一致した場合のみ解の更新をかけています。*8

評価関数の計算時には同じ種類のタイルでマッチングを行う必要があるのですが、最小費用流などを使うと重かったので貪欲に嘘マッチングを行っています。*9

なお、完成図によってはどう頑張っても完成しないパターンもできてしまうのですが、同じ種類のタイルが2枚以上ある場合は適当に入れ替えてあげれば大丈夫です。同じ種類のタイルが存在しないときは困ってしまうので、諦めて焼きなまし自体を行わないようにしました。*10

タイル合わせ

完成図が出来上がったら、どのタイルを持ってくるか決めて実際に合わせていきます。

まずどのタイルを持ってくるか決めるため、重み付きマッチングを行いました。タイルの種類ごとに完成図のタイル（1行・1列分）と今盤面に存在するタイル（固定されていないもの全部）を頂点とする二部グラフを考え、最小費用流を流せばよいです。辺の重みは上記の焼きなましと同じくマンハッタン距離の二乗和を用いました。

ここからIDA*でタイルを合わせていきます。IDA*についてはこの記事が詳しいので詳細はそちらに譲るとして、ここでは簡単に概要のみ説明します。

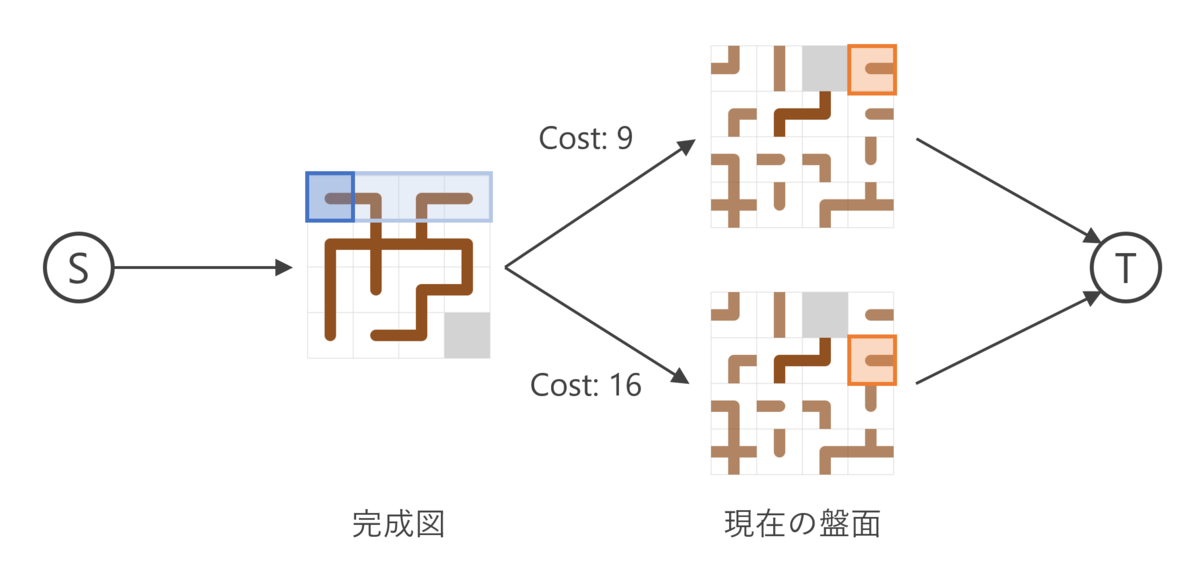
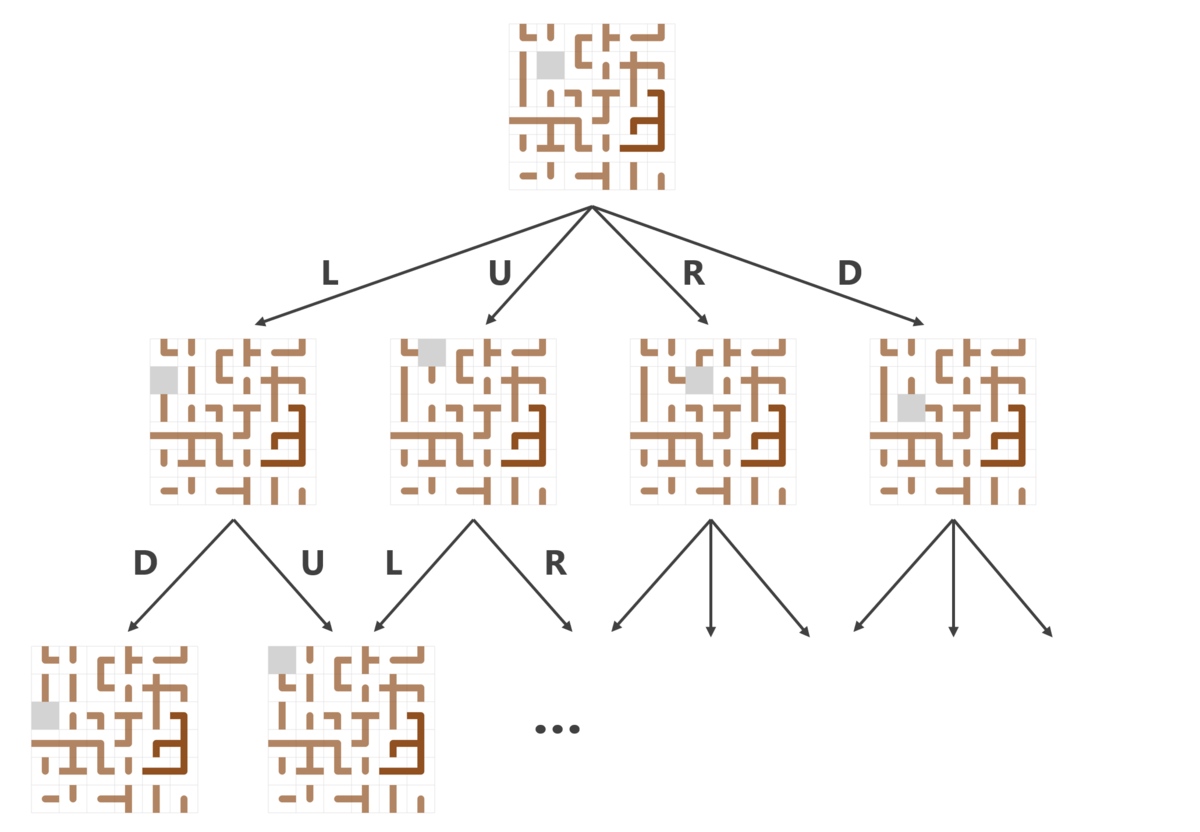
スライドパズルの1盤面を1つの頂点と考えたグラフを探索していきます。このグラフ上をダイクストラ（BFSでも同じです）で探索していけば理論上は完成図までの最短手数が求められます。なのですが、1手につき盤面がだいたい3個くらい増える*11ので、頂点数が指数関数的に増えていって手に負えません。

ここで、例えばタイルを左上に持っていきたいのに初手で右に持っていくような手はなんとなく見込みが薄そうです。そういう手はコストを上乗せして後回しにして、効率の良さそうな手を優先して探索していくダイクストラがA*アルゴリズムです。今回はある盤面に到達するまでの手数を $t$ 、そのときのタイル $i$ の目的地までのマンハッタン距離を $d_i$ として、各盤面のコストを $t+\sum_id_i^{1.5}$ としました。*12

A*は強いのですが欠点もあります。結局はダイクストラなので、キューの中にどんどん要素が詰め込まれていってメモリが厳しくなる上、盤面のコピーコストも馬鹿になりません。*13 そこでA*をBFS風ではなくDFS風にしたのがIDA*です。普通のDFSはどんどん深くまで探索してしまいますが、深さ制限を設定してコストが1のところまで全部DFS、それで見つからなければコストが2のところまで全部DFS……としていくと最短経路を求めることができます。今回はこちらを採用しました。

さらに、探索するときに半分全列挙的な考え方を取り入れたのが双方向IDA*です。例えば普通にDFSで深さ20まで探索しようとするとざっくり $3^{20}=3,486,784,401$ 通りの盤面が出てきて破滅しますが、これを初期盤面と完成図の両方から深さ10ずつ探索して途中で出会うようにすると $2\times3^{10}=118,098$ 通りの盤面で済むようになります。*14

まとめると、

ダイクストラ（＝BFS）：普通に盤面探索
A*：有望な盤面を優先して探索するダイクストラ
IDA*：A*をDFSっぽくやるやつ
双方向IDA*：IDA*を半分全列挙っぽくやるやつ

という感じですね。これを繰り返すことでタイルを全部揃えることができました。

細かいテク

IDA*の仕切り直し

IDA*といえど、やっぱり盤面が大きくなるとすぐ手に負えなくなります。そこで、こちらの記事を参考に、IDA*で探索した状態数が一定数を超えたら、マンハッタン距離の1.5乗和が最も小さい盤面1つだけを残して仕切り直すようにしました。これにより最短手数は保証されなくなりますが、計算量爆発を防ぐことができるようになりました。

Zobrist Hash

こういうボードゲームっぽい問題を考えるときは、Zobrist Hashを使って状態をハッシュ化すると一致判定・重複判定が $O(1)$ で行えるようになって便利です。*15 詳細は割愛しますが、「位置 $(i, j)$ にタイル $k$ が存在する」という全ての $(i, j, k)$ の組について適当な乱数でハッシュを付与してあげて、ある盤面のハッシュは盤面上の全ての要素のハッシュについてXORを取ったもの、としてあげるとよいです。

今回はIDA*の盤面重複除去（同じ盤面を複数回探索するのは無駄なので、最短手数をmapで覚えておいてそれ以上かかっていたら打ち切る）や、双方向IDA*の一致判定にZobrist Hashを使いました。ハッシュの衝突が怖かったのでハッシュ長は128bitとしています。なお、揃えたいタイル以外は全部真っ白なタイルと考えると「微妙に違うけどほとんど同じ」ような盤面を同一視できるのでだいぶ探索効率が良くなりました。

日記

長くなったので別記事にします。結構苦しんで紆余曲折といった内容なのですが、コンテスト中の思考過程を追ってみたい方はよろしければ。

www.terry-u16.net

感想

「木を作る」「スライドパズルを解く」のどちらもさほど斬新な問題というわけではないと思いますが、組み合わせることでこんなに面白い問題になるんですね……！参加者のレベル別に異なる目標が生まれて、幅広い層が楽しめる問題になっていたのではないかと思います。wataさんの問題は毎回解き応えのある良問ばかりで本当に凄いです。*16

スライドパズルなんてプログラムはおろか手ですら解いたことがなかったので「こんなの天才パズルerじゃないと無理だろ……」と思っていたのですが、思った以上に良い成績を出すことができて良かったです。前回のAHC010ではレーティング2800目前で足踏みしてしまっていましたが、今回リベンジを果たしてついに赤コーダーになれたのでとても嬉しいです。またZobrist HashやIDA*など、初めて使うアルゴリズムを上手く活用できたのも褒めポイントですね。

赤コーダーになれたのでレーティング的には一区切りですが、もちろん今後もヒューリスティックコンテストには積極的に参加していくつもりです。次回のAHCもとても楽しみにしています！

*1:今回初めて使ったので不安でしたが、うまく動いてくれました。

*2:連結でなくなる・閉路ができるなど。

*3:Link-Cut Treeを使えばO(logN)でできる気もしますが、どうせ定数倍が重いこと、また何より実装できる気がしなかったことから採用しませんでした。

*4:一番大きい連結成分以外も評価したい・ループができてもいきなり0点にはしたくないみたいな気持ちです。

*5:高速に初期解が見付けられるようになったのはもちろん、局所解にハマりにくくなったため後述する完成図の改変も上手く行くようになりました。

*6:4x4の時点で既にキツいはず。

*7:完成図の改変が結構効いて、暫定37M点から40M点以上へ一気に点数を上げることができました。

*8:理論上は先ほどの完成図作成パートなしでも作れるはずですが、マッチングが重いのか評価関数が良くないのか、完成図作成パートなしだと時々タイル数合わせに失敗していました。

*9:これでもそこそこいいマッチングが得られるはずで、高速化の恩恵によりスコアも1000ケースで0.5%ほど上昇しました。

*10:ちゃんと偶奇チェックしてあげても良いのですが、その時には既に盤面が小さくなっているのでそもそも焼きなましの余地がほとんどなくなっているはず。

*11:タイルは4方向に動かせますが、LRやUDのような移動は無駄なので省いています。

*12:1.5乗はkusanoさんの記事を参考にしましたが、なぜ1.5乗が良かったのかは謎。なお1.5乗とすると最短手数を取りこぼす可能性がありますが気にしていません。

*13:と思っています。3秒そこらの問題でどっちが速いかは未検証。

*14:実際には完成図側はIDA*ではなくIDDFSを使いました。単に面倒だったので。

*15:と言いつつ、実際のヒューリスティックコンテストで活用したのは初めてです。

*16:そしてwriter解も強すぎました……。

TERRYのブログ

最近は競技プログラミングにお熱。

AtCoder Heuristic Contest 011 (AHC011) 解説