THIRDプログラミングコンテスト2021（AtCoder Heurisitic Contest 007）お疲れ様でした。企業AHCが増えてきて嬉しいです。コンテストトップページの企業紹介が強すぎてびっくりしてしまいましたが……。この調子でAHCがどんどん盛り上がってくれると嬉しいです。

というわけで今回も解説を書いてみます。あくまで解法の一例で、今回紹介する方法以外にも無数の解法があることに注意してくださいね。

f:id:terry_u16:20211215204914p:plain — ビジュアライザ (seed=0)

問題概要

なるべくコストの小さい全域木を作ってね。ただし辺のコストは1本ずつ順番に教えるから、使うかどうかはその場で判断してね。

atcoder.jp

最小全域木問題！辺のコストが事前に全て分かっていればクラスカル法なりプリム法なりをやるだけなんですが、オンラインクエリ化するだけで一気に難しくなりますね。

最小全域木問題を知らない方にとってはちょっと辛かったかもしれませんが、例えば「Union-Findで頂点を管理し、辺の両端の頂点が別のグループに属していたらその辺を採用する」といった方針でも正当な解を得ることができます。そこから「明らかに長すぎる辺は採用しない」等の工夫もできますね。このようにアルゴリズムを知らなくても楽しめるのはヒューリスティックコンテストの良いところだと思います。

前提知識

クラスカル法

方針

辺を使ったときと使わなかったときについてそれぞれ想定される最終的なコストの期待値を求めて、よりお得な方を採用していけば良さそうです。辺のコストがオンラインで与えられるので期待値の計算が難しいのですが、 $i$ 番目の辺のコストは $\mathrm{rand}(d_i, 3d_i)$ で与えられるという事前情報があるため、今回はモンテカルロ法により期待値を近似的に求めていくことにします。

モンテカルロ法とは

以下の問題を考えます。

$1$ 以上 $6$ 以下の整数の目が全て等確率で得られるサイコロがある。このサイコロを $10$ 回振るとき、出る目の総和の期待値を求めよ。

解法1

サイコロを $1$ 回振ったときの期待値は $\frac{1}{6}\times 1+\frac{1}{6}\times 2 + \cdots + \frac {1}{6} \times 6 = \frac{7}{2}$ であるので、答えはそれを $10$ 倍した $35$ です。

解法2

解法1では期待値を計算して求めましたが、実際にサイコロを振ってみるという解法も考えられます。やってみましょう。

import random

# サイコロを振る回数
N = 10

# 出た目の合計
dice_sum = 0

for i in range(N):
    dice = random.randint(1, 6)
    dice_sum += dice
    print(f"{i + 1:2}回目: {dice:2}")

print(f"合計  : {dice_sum:2}")

実行結果

 1回目:  4
 2回目:  5
 3回目:  1
 4回目:  1
 5回目:  3
 6回目:  5
 7回目:  6
 8回目:  6
 9回目:  4
10回目:  3
合計  : 38

当然1回やるだけだとブレまくりますが、試行回数を増やしていくとだんだん正しい値に収束していきます。

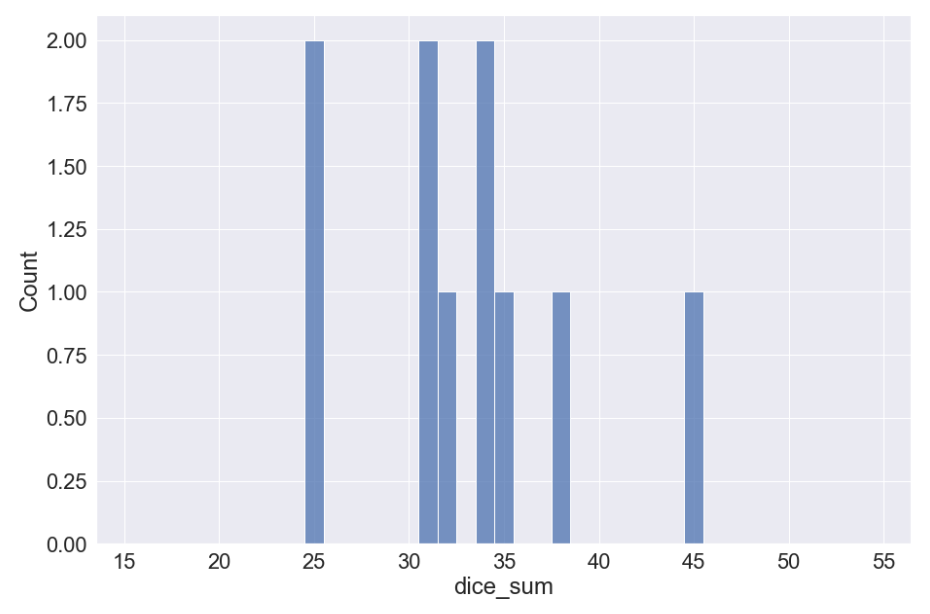
f:id:terry_u16:20211215171126p:plain — 試行回数10回：平均値33.00

f:id:terry_u16:20211215171221p:plain — 試行回数100回：平均値34.52

f:id:terry_u16:20211215171301p:plain — 試行回数1000回：平均値35.13

f:id:terry_u16:20211215171340p:plain — 試行回数10000回：平均値35.02

10000回繰り返したところで平均値35.02が得られました。厳密に正しい答えではないですが、実用上はこれで十分なことも多いです。

サイコロの例では手計算でも簡単に解が求められましたが、モンテカルロ法は解析的に解を求めることが難しい問題で威力を発揮します。ということで、THIRDコンの問題にモンテカルロ法を適用してみましょう。

モンテカルロ法の適用

「方針」の項目で書いたように、辺を採用した場合と採用しなかった場合の最終的なコストの期待値の近似値をモンテカルロ法により求めていきます。未知の辺のコストを予め $\mathrm{rand}(d_i, 3d_i)$ でランダムに生成しておいて、このランダムな辺を使って毎回クラスカル法により最小全域木を求めればよいです。サイコロの例からも分かるように、ランダムな辺 $M$ 本を $1$ セット作るだけだと結果がブレるので、これを $S$ セット作ってコストの平均を見ることにします。

具体的には以下のようなアルゴリズムになります。

予め $M$ 本のランダムなコストの辺を $S$ セット作成しておく。*1 $i$ 番目の辺のコストは $\mathrm{rand}(d_i, 3d_i)$ により求める。
$i$ 番目の辺の真のコスト $l_i$ を受け取る。
頂点 $u_i$ と頂点 $v_i$ が既に同じ連結成分に入っている場合は、辺を採用せずに2.に戻る。
$i$ 番目の辺を使ったとき、最終的なコストがいくらになるかクラスカル法によりシミュレートする。 $i$ 番目の辺を使ってコスト $l_i$ で頂点 $u_i$ と頂点 $v_i$ を繋いだ後、1.で作成したランダムな辺の $i+1$ 番目以降を使ってクラスカル法を行えばよい。
$i$ 番目の辺を使わなかったとき、最終的なコストがいくらになるかクラスカル法によりシミュレートする。 $i$ 番目の辺を使わずに、1.で作成したランダムな辺の $i+1$ 番目以降を使ってクラスカル法を行えばよい。最終的にグラフが連結とならないケースに注意する。
1.で作成した $S$ セットの辺について、4.と5.を繰り返す。 $j$ 番目のセットでの最終的なコストをそれぞれ $c_j, \bar c_j$ とおく。
$i$ 番目の辺を採用したときのコストの総和 $\sum_{j=1}^{S}c_j$ と採用しなかったときのコストの総和 $\sum_{j=1}^{S}\bar c_j$ を比較し、 $\sum_{j=1}^{S}c_j \le \sum_{j=1}^{S}\bar c_j$ であれば $i$ 番目の辺を採用する。
2.に戻る。

コードにすると以下のようになります。できるだけ高速化してセット数 $S$ を稼ぎたいので、今回はC++を採用しました。*2 コードテストで実行時間を計測し、 $S=14$ に設定しました。

#include <algorithm>
#include <atcoder/dsu>
#include <cmath>
#include <iostream>
#include <random>
#include <utility>
#include <vector>

using namespace std;
using namespace atcoder;

// 頂点の数
constexpr int N = 400;
// 辺の数
constexpr int M = 1995;
// ランダムな辺の生成数
constexpr int EDGE_SET_COUNT = 14;
// 乱数のシード値
constexpr int RANDOM_SEED = 42;
// INF（小さめ）
constexpr int INF = 10000000;

/// 2次元平面上の座標を表す構造体。
struct coordinate {
    int x;
    int y;

    coordinate(int x, int y) : x(x), y(y) {}

    /// 2頂点間のユークリッド距離を求める。
    int get_dist(const coordinate &other) {
        int dx = x - other.x;
        int dy = y - other.y;
        double d = round(sqrt(dx * dx + dy * dy));
        return static_cast<int>(d);
    }
};

/// 入力を表す構造体。
struct input {
    int n;
    int m;
    vector<coordinate> coordinates;
    vector<pair<int, int>> edges;

    input(int n, int m, vector<coordinate> &&coordinates, vector<pair<int, int>> &&edges)
        : n(n), m(m), coordinates(coordinates), edges(edges) {}
};

// ==== プロトタイプ宣言 ====

input read_testcases();
void solve(const input &input);
vector<vector<int>> generate_random_dists(const input &input, int count, int random_seed);
vector<int> calc_euclidean_dists(const input &input);
bool decide_use_or_not(const input &input, int edge_index, int edge_distance, dsu &union_find,
                       const vector<vector<int>> &random_dists);
vector<int> get_sorted_edge_indice(int start_index, const vector<int> &distances);
int kruskal(const input &input, dsu &union_find, const vector<int> &sorted_edge_indice, const vector<int> &distances);

// ==== プロトタイプ宣言ここまで ====

/// エントリポイント。
int main() {
    input input = read_testcases();
    solve(input);
}

/// テストケースを読み込む。
input read_testcases() {
    // 点の座標(x, y)の読み込み
    vector<coordinate> coordinates;
    for (int i = 0; i < N; i++) {
        int x, y;
        cin >> x >> y;
        coordinate coordinate(x, y);
        coordinates.push_back(coordinate);
    }

    // 辺(u, v)の読み込み
    vector<pair<int, int>> edges;
    for (int i = 0; i < M; i++) {
        int u, v;
        cin >> u >> v;
        edges.push_back(make_pair(u, v));
    }

    input input(N, M, move(coordinates), move(edges));
    return input;
}

/// 問題を解く。
void solve(const input &input) {
    // ランダムな辺のリストを生成
    vector<vector<int>> random_dists = generate_random_dists(input, EDGE_SET_COUNT, RANDOM_SEED);

    // 頂点の連結状態を管理するDSU (=Union-Find)
    dsu union_find(input.n);

    // 各辺について採用するかしないか判断していく
    for (int edge_index = 0; edge_index < input.m; edge_index++) {
        // i番目の辺の長さを読み込む
        int edge_distance;
        cin >> edge_distance;

        // 採用するかしないか判断
        bool use = decide_use_or_not(input, edge_index, edge_distance, union_find, random_dists);

        if (use) {
            // 採用する場合は辺で繋げる
            auto [u, v] = input.edges[edge_index];
            union_find.merge(u, v);
            cout << 1 << endl;
        } else {
            cout << 0 << endl;
        }
    }
}

/// ランダムな辺の長さのリストをcount個生成する。
/// 各辺の長さは、辺のユークリッド距離をdとしてd以上3d以下のランダムな値とする。
vector<vector<int>> generate_random_dists(const input &input, int count, int random_seed) {
    // 乱数生成器（メルセンヌ・ツイスタ）の初期化
    mt19937 mt(random_seed);

    // ユークリッド距離を求めておく
    vector<int> euclidean_dists = calc_euclidean_dists(input);

    // 辺の長さの2次元配列
    // M要素の配列がcount個入る
    vector<vector<int>> random_dists(count);

    // 辺の生成
    for (int i = 0; i < count; i++) {
        for (int j = 0; j < input.m; j++) {
            // d以上3d以下の範囲でランダムに辺の長さを決める
            // uniform_int_distributionは指定範囲の整数を一様ランダムに生成するクラス
            uniform_int_distribution<int> rand(euclidean_dists[j], 3 * euclidean_dists[j]);
            int dist = rand(mt);
            random_dists[i].push_back(dist);
        }
    }

    return random_dists;
}

/// 全ての辺のユークリッド距離を計算する。
vector<int> calc_euclidean_dists(const input &input) {
    vector<int> distances;

    for (int i = 0; i < input.m; i++) {
        auto [u, v] = input.edges[i];
        coordinate p = input.coordinates[u];
        coordinate q = input.coordinates[v];
        int dist = p.get_dist(q);
        distances.push_back(dist);
    }

    return distances;
}

/// edge_index番目の辺を採用するかしないか判断する。
bool decide_use_or_not(const input &input, int edge_index, int edge_distance, dsu &union_find,
                       const vector<vector<int>> &random_dists) {
    auto [u, v] = input.edges[edge_index];

    // 既に連結だったら採用しない
    if (union_find.same(u, v)) {
        return false;
    }

    // 採用した場合・しなかった場合のコストの和
    int use_cost_sum = 0;
    int pass_cost_sum = 0;

    // 各ランダムケースに対して、辺を採用する場合と採用しない場合のコストを計算する
    for (int i = 0; i < random_dists.size(); i++) {
        // 予め辺のedge_index+1番目以降のインデックスを距離の昇順で並べ替えておく
        // クラスカル法を2回やるので前計算した方が高速
        vector<int> sorted_edge_indice = get_sorted_edge_indice(edge_index + 1, random_dists[i]);

        // 辺を採用する場合のコスト計算
        // Union-Findをコピーしておく
        dsu union_find_use(union_find);
        union_find_use.merge(u, v);

        // 採用する場合のコストは、edge_index番目の辺のコストとそれ以降のクラスカル法のコストの和
        int use_cost = edge_distance + kruskal(input, union_find_use, sorted_edge_indice, random_dists[i]);
        use_cost_sum += use_cost;

        // 辺を採用しない場合のコスト計算
        dsu union_find_pass(union_find);

        // 採用しない場合のコストは、edge_index+1番目以降のクラスカル法のコスト
        int pass_cost = kruskal(input, union_find_pass, sorted_edge_indice, random_dists[i]);
        pass_cost_sum += pass_cost;
    }

    // 採用した場合のコストの総和が採用しない場合のコストの総和以下であれば採用
    bool use = use_cost_sum <= pass_cost_sum;
    return use;
}

/// start_index以降の辺のインデックスを距離の昇順で並べ替える。
vector<int> get_sorted_edge_indice(int start_index, const vector<int> &distances) {
    // start_index以降のインデックスを列挙
    vector<int> indice;
    indice.reserve(distances.size() - start_index);

    for (int i = start_index; i < distances.size(); i++) {
        indice.push_back(i);
    }

    // 辺の距離の昇順でインデックスを並び替える
    sort(indice.begin(), indice.end(), [&](int a, int b) { return distances[a] < distances[b]; });

    return indice;
}

/// クラスカル法により最小全域木問題を解き、コストの総和を返す。
/// sorted_edge_indiceはdistanceの昇順でソート済みである必要がある。
/// グラフを連結にできない場合はINFを返す。
int kruskal(const input &input, dsu &union_find, const vector<int> &sorted_edge_indice, const vector<int> &distances) {
    // 普通にクラスカル法をやる
    int cost_sum = 0;

    for (int i = 0; i < sorted_edge_indice.size(); i++) {
        int index = sorted_edge_indice[i];
        auto [u, v] = input.edges[index];

        if (!union_find.same(u, v)) {
            union_find.merge(u, v);
            cost_sum += distances[index];
        }
    }

    // グラフが連結になったかどうか判断
    bool connected = union_find.size(0) == input.n;

    if (connected) {
        return cost_sum;
    } else {
        // 連結でない場合はINFを返す
        // オーバーフローに注意
        return INF;
    }
}

これを提出すると、14,146,906,243点が得られました。本番54位相当で黄perf（β）ですね。工夫次第でもっと伸ばすこともできます。

atcoder.jp

私が本番中に提出したコードはこんな感じ（14,194,465,166点、22位）です。ほとんど上の解法のままで高速化くらいしかしていません。 $S$ は $50$ ～ $80$ くらい？回ってそうです。Rustですが参考までに。*3

atcoder.jp

おまけ：辺のコストを2dとするとダメな理由

おまけです。

直感的には $i$ 番目の辺のコストを $2d_i$ で固定し、同じようにクラスカル法を回しても良い気がしますが、これだとあまりスコアが伸びません。実際にやってみたところ、13,885,749,353点（本番245位相当）止まりでした。

atcoder.jp

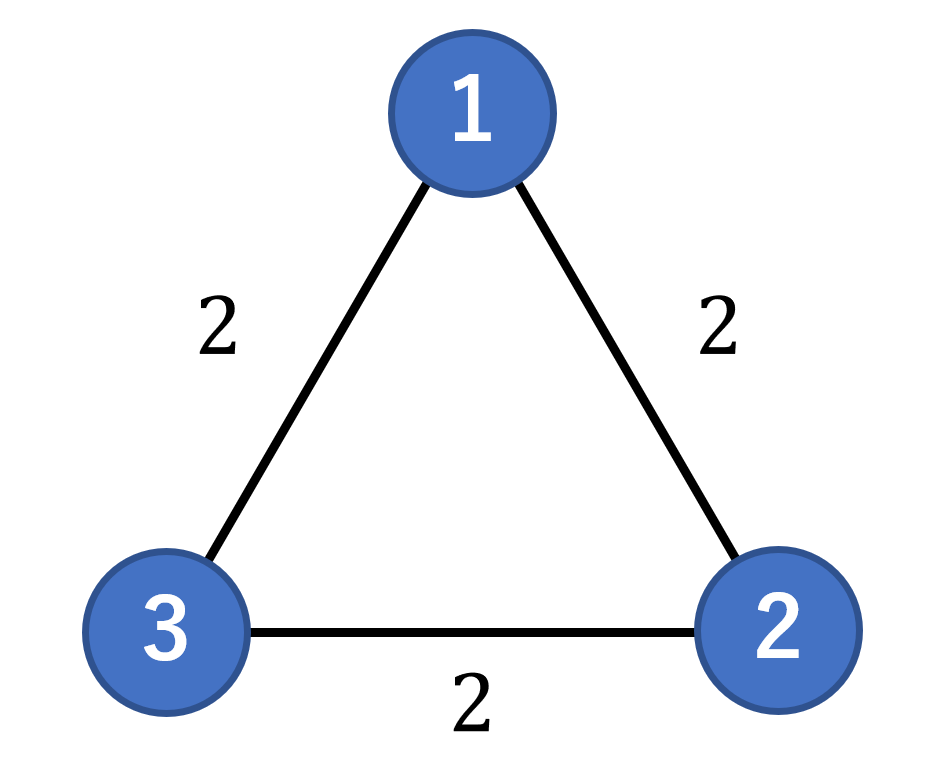
結論から言うと、辺のコストを $2d_i$ とすると最終的なコストを高く見積もりすぎてしまうのが原因です。例として以下のようなグラフを考えてみましょう。

f:id:terry_u16:20211215182138p:image:w400 — N=3, M=3のグラフ

各辺のコスト $l_1, l_2, l_3$ は $1$ から $3$ までのランダムな実数値を取るものとします。各辺のコストを全て $2$ で固定した場合、最小全域木を作るには辺を $2$ 本使えばよいので、最終的なコストは $4$ です。

f:id:terry_u16:20211215183022p:image:w400 — l1=l2=l3=2とした場合

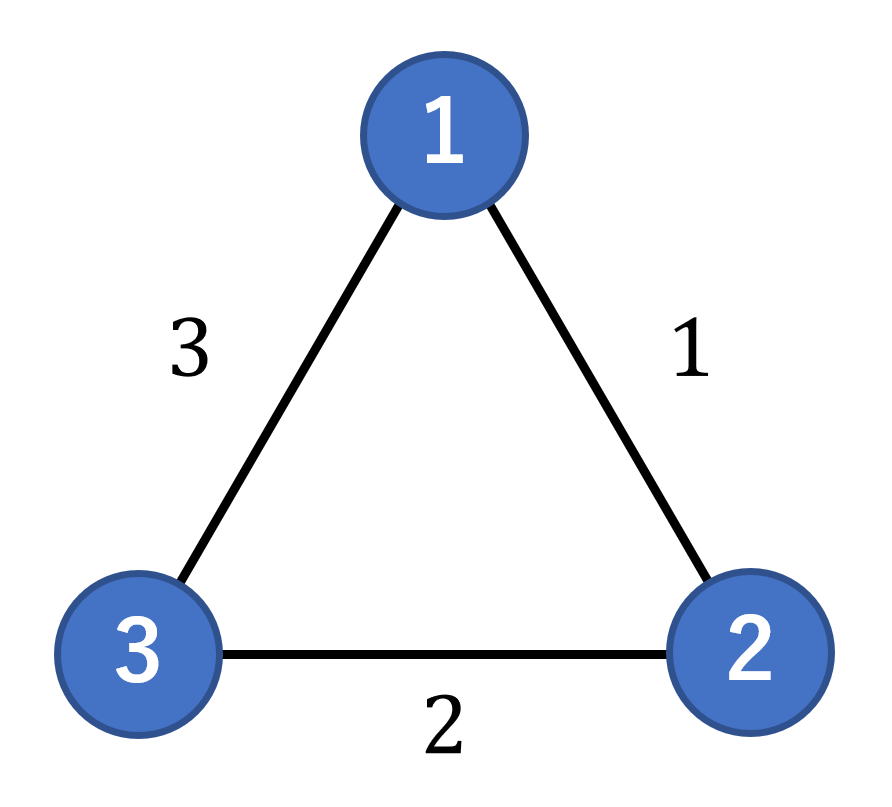
ここで、 $l_1=1, l_2=2, l_3=3$ となったケースを考えましょう。

f:id:terry_u16:20211215182808p:image:w400 — l1=1, l2=2, l3=3となったケース

最小全域木を作るとき、3本の辺の中からコストの小さい2本を選ぶことができます。したがって最もコストの高い $l_3$ を捨てることができ、その分使用する辺のコストの平均値が下がるのです。辺のコストを $2d_i$ とした場合、これを考慮することができないために、最終的なコストを高く見積もってしまいます。*4