センサーサイズとボケサイズ（後編）

f:id:terry_u16:20180930183254j:plain
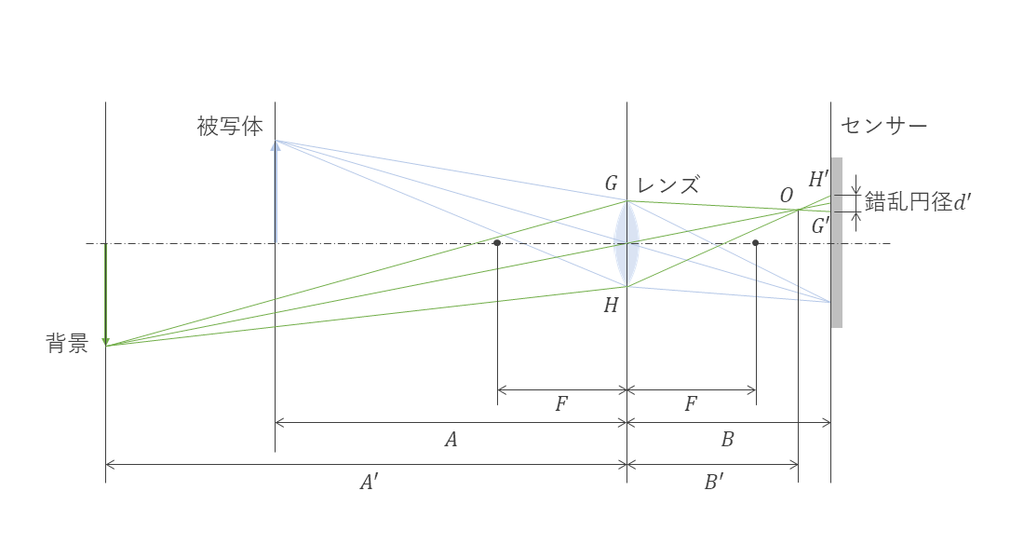
前編では、レンズの有効口径を使ってボケの大きさを見積もってきました。
www.terry-u16.net
この方法は、被写体との距離を変えずにレンズの焦点距離を変えたとき、どのくらいボケの大きさが変わるかを見積もるのに便利でした。
それでは、レンズの焦点距離を変えずに被写体との距離を変えたときは、どのように考えれば良いのでしょうか。

光学素子としてのレンズの基礎知識
- レンズの公式
- ボケのしくみ
ボケ量の定量的計算
- 点光源の錯乱円径
- 被写体との距離を変えてAPS-Cで撮るときのボケ量
まとめ

光学素子としてのレンズの基礎知識

ボケの大きさを議論するためには、まずレンズの基礎知識についておさらいしておく必要があります。少々長いですが、どうぞお付き合いください。

レンズの公式

f:id:terry_u16:20180930115838p:plain
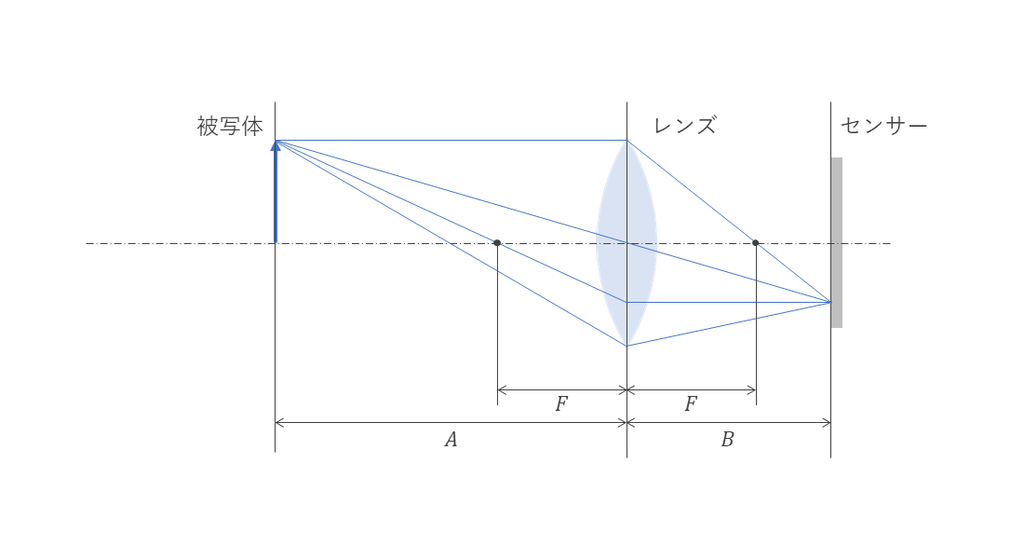
このクソポンチ絵は、被写体のてっぺんから出た光が焦点距離 $F$ のレンズを通ってカメラのイメージセンサーに像を結ぶまでの光の経路を示しています。中学校で学んだのを覚えているという方も多いでしょう。理想的な凸レンズでは、

光軸に平行な光線は、レンズを通ったのち焦点を通る。
焦点を通った光線は、レンズを通ったのち光軸に平行な光線となる。
レンズの中心を通った光は、そのまま角度を変えることなく直進する。

という性質があるため、それを踏まえて作図してあげるとこんな絵になります。実際のカメラレンズはもっと複雑な光学系をしていますが、基本的な原理としては同じです。

余談ですが、最近RTX2080Ti効果でレイトレーシングが話題ですね。レイトレーシングは、目からたくさんビームを飛ばし、屈折や反射を繰り返した先に何が見えるかをトレースすることで3DCGを描画する手法です。現実世界では光源からの光が反射を繰り返して網膜に飛び込んでくるのですが、それだと目に入ってこない光もわざわざ計算することになり計算量が膨大になるため、レイトレーシングではそれを逆にトレースすることで計算量を抑えています。それでも光の反射*1が増えるごとに計算量が爆発的に増えるのですが。
映画制作なんかで大規模サーバー群を使って数時間～数日かけて行っていた処理がリアルタイムで行えるようになるとは良い時代になったものですね。今後が楽しみです。

閑話休題。

さて、このようにガチピンのとき、焦点距離 $F$ と、被写体からレンズまでの距離 $A$ 、そしてレンズからイメージセンサーまでの距離 $B$ には、次のような関係が成り立ちます。
$\displaystyle \frac 1 F=\frac 1 A + \frac 1 B \tag{1}$
これがレンズの公式です。この式も高校あたりで習った方が多いと思います。実際のカメラレンズでは、この式を満たすようレンズを前後に動かして $A,B$ を変化させることでピントを合わせているのですね。*2

ボケのしくみ

f:id:terry_u16:20180930115851p:plain
被写体にピントを合わせたとき、背景にある点光源からの光はどのような経路を辿るのでしょうか。それを表したのがこちらのクソポンチ絵です。 $A$ が $A'$ に変化したので、 $B$ も $B'$ に変わっています。その結果、光線はセンサーよりも手前で結像し、センサーには円形に“ボケ”た光が届きます。これがボケの発生する原理ですね。この円のことを錯乱円といいます。錯乱円の径が大きくなればなるほど、ボケも大きくなります。

f:id:terry_u16:20180930115912p:plain
ちなみに、 $\triangle{OGH}\sim\triangle{OG'H'}$ *3であるため、レンズの有効口径 $D$ と錯乱円径 $d$ （＝ボケの大きさ）は比例します。有効口径が半分になれば、錯乱円径も半分になります。これが前回お話しした、有効口径とボケの大きさが比例関係にある理由ですね。

ボケ量の定量的計算

点光源の錯乱円径

さて、ここからはボケの大きさが数式を使ってどのように表されるか導出してみましょう。数式が多くなりますが、そんなに複雑な計算は出てこないので、どうぞ寝ずにお付き合いください。
まず、式 $(1)$ を変形すると、レンズからイメージセンサーまでの距離 $B$ は次式で表されます。
$\displaystyle B=\frac 1{\frac 1 F - \frac 1 A} \tag{2}$
背景の点光源についても同様に、
$\displaystyle B'=\frac 1{\frac 1 F - \frac 1 {A'}} \tag{3}$
ここで、 $\triangle{OGH}\sim\triangle{OG'H'}$ より、レンズの有効口径 $D$ と錯乱円径 $d$ の間には、
$\displaystyle D:d=B':\left(B-B'\right)\tag{4}$
の関係が成り立つので、
$\displaystyle d=D \cdot \frac {B-B'} {B'} \tag{5}$
また、レンズの有効口径 $D$ は、前編で示したように焦点距離 $F$ と絞り $f_n$ を用いて $D=F / {f_n}$ と表されるので、
$\displaystyle d=\frac F {f_n} \cdot \frac {B-B'} {B'} \tag{6}$
式 $(6)$ に式 $(2)$ および式 $(3)$ を代入して整理すると、
$\displaystyle d=\frac F {f_n} \cdot \frac {\left(A'-A\right)F} {\left(A-F\right)A'} \tag{7}$
複雑になってきたので、簡単のため、背景の点光源は無限遠に存在するとして考えます。
$\displaystyle d_{\infty}= \lim_{A'\rightarrow \infty}d=\frac {F^2} {\left(A-F\right){f_n}} \tag{8}$
やっと出ました。これが、無限遠に存在する点光源の錯乱円径の式です。ただ、錯乱円径が同じでも、センサーサイズによって写真として残るボケの大きさは変わりますので、センサーの対角線長さ $L_D$ で正規化して、センサーの対角線の長さに対するボケ直径の比 $d_n$ を定義してあげましょう。
$\displaystyle d_n= \frac {d_{\infty}} {L_D}=\frac {F^2} {\left(A-F\right){f_n}{L_D}} \tag{9}$
式 $(9)$ より、一般に言われている以下の定説が正しいことが分かります。被写体にピントが合っている（実像が存在する）状態では、 $A\gt F$ であることに注意してください。

F値 $f_n$ を小さくするとボケやすくなる。
レンズの焦点距離 $F$ を長くするとボケやすくなる。
被写体に近付く（ $A\rightarrow F$ ）とボケやすくなる。

また、前編の内容についても、センサーサイズ $L_D$ が1.6倍になったとき、同じ画角を得るために焦点距離 $F$ も1.6倍すれば、同じ絞り値でだいたい1.6倍の径のボケを得ることができる、ということがこの式から言えます。*4

被写体との距離を変えてAPS-Cで撮るときのボケ量

お疲れ様でした。ここまで来れば楽勝です。*5
「フルサイズと同じレンズで、被写体との距離を変えてAPS-Cで撮る」とき、フルサイズと写る範囲を同じにするには、被写体との距離 $A$ を1.6倍*6にすれば良いです。センサーサイズ $L_D$ も変化することに気を付けると、ボケの径は、
$\displaystyle\frac {d_n'}{d_n}=\frac{1.6\left(A-F\right)}{1.6A-F}\tag{10}$
倍になります。マクロレンズで接写でもしない限り、被写体との距離 $A$ は焦点距離 $F$ の数十倍であることが多いため、 $F$ はほぼ無視してよく、
$\displaystyle\frac {d_n'}{d_n}\approx 1\tag{11}$
となります。なんと、後ろに引いて撮った場合、同じレンズであればセンサーサイズが変わっても写真に写るボケの大きさはほとんど変わらない*7のです。なんとなく直感と異なりますが、数式は嘘をつきません。これについては筆者も驚きました。
ただし、「背景の点光源は無限遠に位置する」という条件を外せば、フルサイズの方がボケやすくなります。詳細は割愛しますが、気になる方はExcelなりで式 $(7)$ の $d/{L_D}$ を計算してみてください。

まとめ

前編から2回にわたり、ボケの大きさについて考えてきました。結論としては、

被写体を同じ設定・同じフレーミングで撮るとき、

焦点距離を変化させて同じ画角にする場合、ボケの大きさはセンサーサイズに比例する。（フルサイズとAPS-Cでは約1.3段分、フルサイズとm4/3では約2段分の違い）
焦点距離を変化させず被写体との距離を変えた場合、ボケの大きさはほとんど変わらない。（ただし、背景が無限遠にある場合のみ）

ということです。同じ画角で勝負するならフルサイズの方が有利ですが、焦点距離を変えずに被写体との距離で調整するならどのフォーマットでもだいたい同じです。ただし、後ろに引けるような状況であればフルサイズも焦点距離の長いレンズに変更できるため、やはりフルサイズの方が有利ということは変わらなさそうです。

ただし、ボケれば良いってものでもありません。ボケやすいということは、パンフォーカスにしづらいということです。被写体によっては、高価で大きくて重いフルサイズのシステムで撮影しても、より軽量なAPS-Cやm4/3と大差ないということも多いです。
何を撮りたいかを明確にして、自分に合ったカメラシステムを作り上げていきましょう。

*1:厳密にはマットな面での反射時に生じる拡散

*2:レンズによっては焦点距離まで微妙に変わっちゃったりしますが。

*3:英語文化圏では相似を∽ではなく～で表すらしい。

*4:厳密には $1/(A-F)$ の影響がありますが、マクロ撮影以外では $A\gg F$ とみなせるため、あまり気にしなくても実用上問題ありません。ちなみに等倍マクロでは $A=2F$ となります。

*5:と言っておきながら初版では大きなミスをするという不覚

*6:キヤノンの場合

*7:錯乱円径は小さくなるが、センサーサイズも小さくなるので、最終的に画像として残るボケの大きさは変わらない。

TERRYのブログ

最近は競技プログラミングにお熱。